Complex reasoning tasks, such as commonsense reasoning and math reasoning, have long been the Achilles heel of Language Models (LMs), until a recent line of work on Chain-of-Thought (CoT) prompting [6, 7, 8, i.a.] brought striking performance gains.
In this post, we introduce a new reasoning franework, Faithful CoT, to address a key shortcoming of existing CoT-style methods – the lack of faithfulness. By guaranteeing faithfulness, our method provides a reliable explanation of how the answer is derived. Meanwhile, it outperforms vanilla CoT on 9 out of the 10 datasets from 4 diverse domains, showing a strong synergy between interpretability and accuracy.
Chain-of-Thought (CoT) Prompting
Chain-of-Thought (CoT) prompting [7] is a type of few-shot learning technique, where an LM is prompted to generate a reasoning chain along with the answer, given only a few in-context exemplars (right). This has remarkably boosted LMs’ performance on a suite of complex reasoning tasks, compared to standard prompting [1], where the model is prompted to generate only the answer but not the reasoning chain (left).
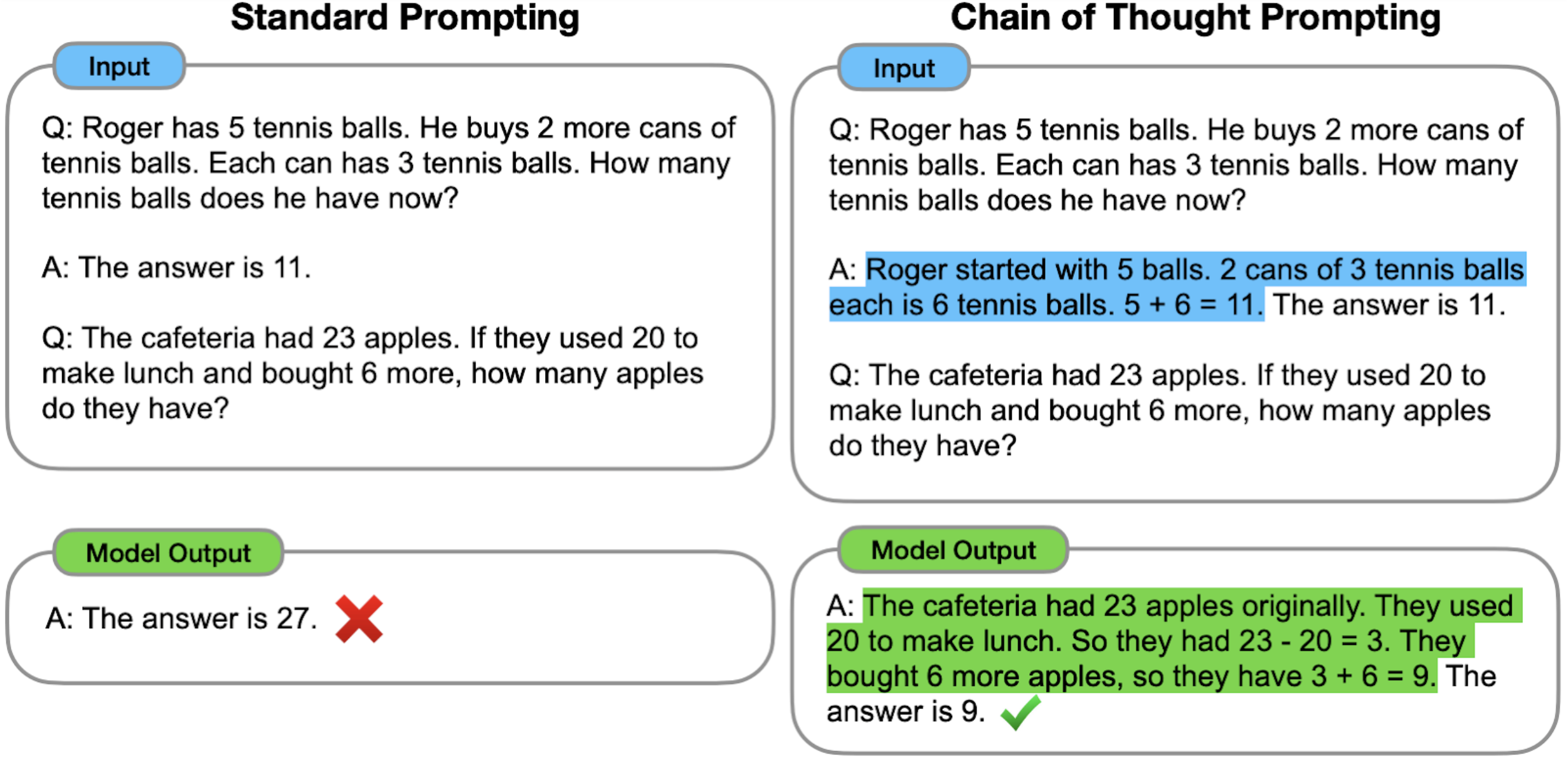
Lack of Faithfulness in CoT
In addition to accuracy improvement, CoT is claimed to “provide an interpretable window into the behavior of the model”. But are these CoT reasoning chains actually good “explanations”?
Not necessarily, because they lack one fundamental property of interpretability, faithfulness:
Faithfulness: An explanation (e.g., the generated reasoning chain) should accurately represent the reasoning process behind the model’s prediction (i.e., how the model arrives at the final answer)”[3].
In most existing CoT-style methods, the final answer does not necessarily follow from the previously generated reasoning chain, so there is no guarantee on faithfulness:
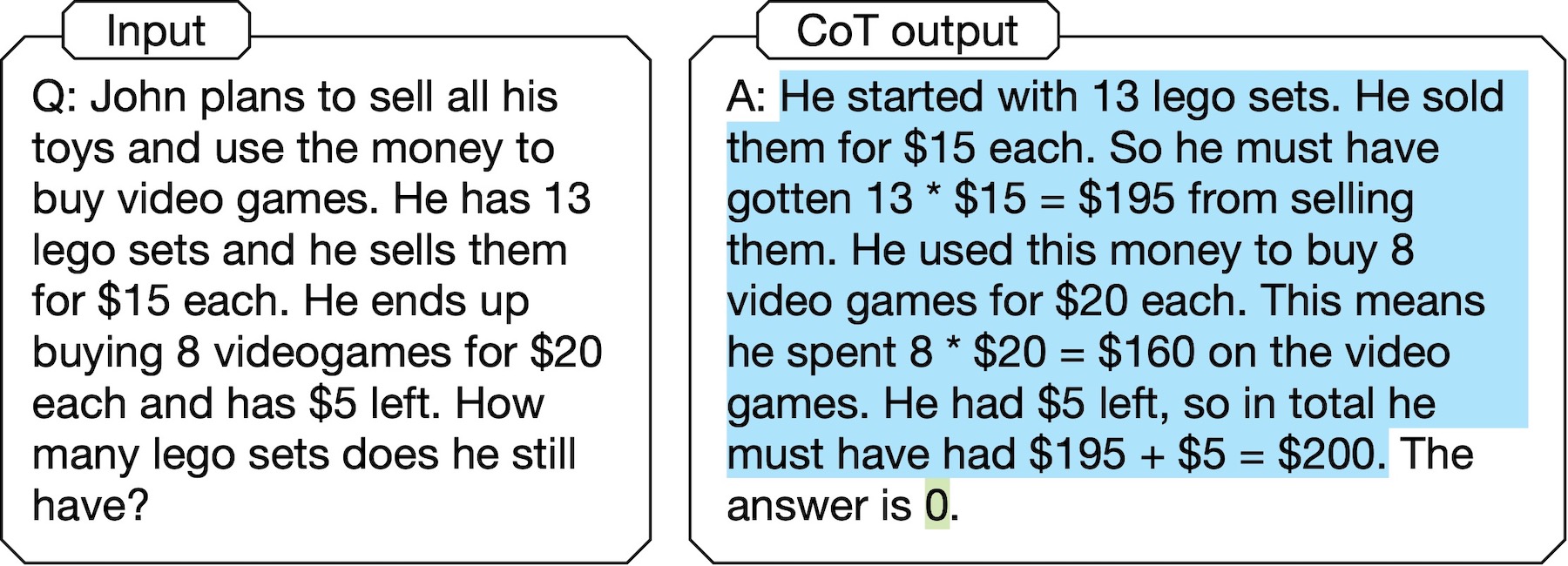
In the above example of CoT output, the answer “0” is not even mentioned in the reasoning chain. In other words, the LM doesn’t really get to the answer in the way that it states to. This, along with more examples in our paper and other recent studies (e.g., [5]), illustrates that such CoT methods are not truely self-interpretable.
The lack of faithfulness in CoT can be dangerous in high-stake applications because it can give a false impression of “inherent interpretiblity”, whereas there is indeed no causal relationship between the reasoning chain and the answer. Even worse, when an unfaithful explanation looks plausible (i.e., convincing to humans), this makes it easier for people (e.g., legal practitioners) to over-trust the model (e.g., a recidivism predictor) even if it has implicit biases (e.g., against racial minorities) [4].
Our method: Faithful CoT
We propose Faithful CoT, a faithful-by-construction prompting framework where the answer is derived by deterministically executing the reasoning chain. Specifically, we break down a complex reasoning task into two stages: Translation and Problem Solving.
During Translation, an LM translates a Natural Language query into a reasoning chain, which interleaves Natural Language and Symbolic Language. The Natural Language component is a decomposition of the original query into multiple simpler, interdependent subproblems. Then, each subproblem is solved in a task-dependent Symbolic Language, such as Python, Datalog, or Planning Domain Definition Language (PDDL). Next, in the Problem Solving stage, the reasoning chain is executed by a deterministic solver, e.g., a Python/Datalog interpreter, or a PDDL planner, to derive the answer.
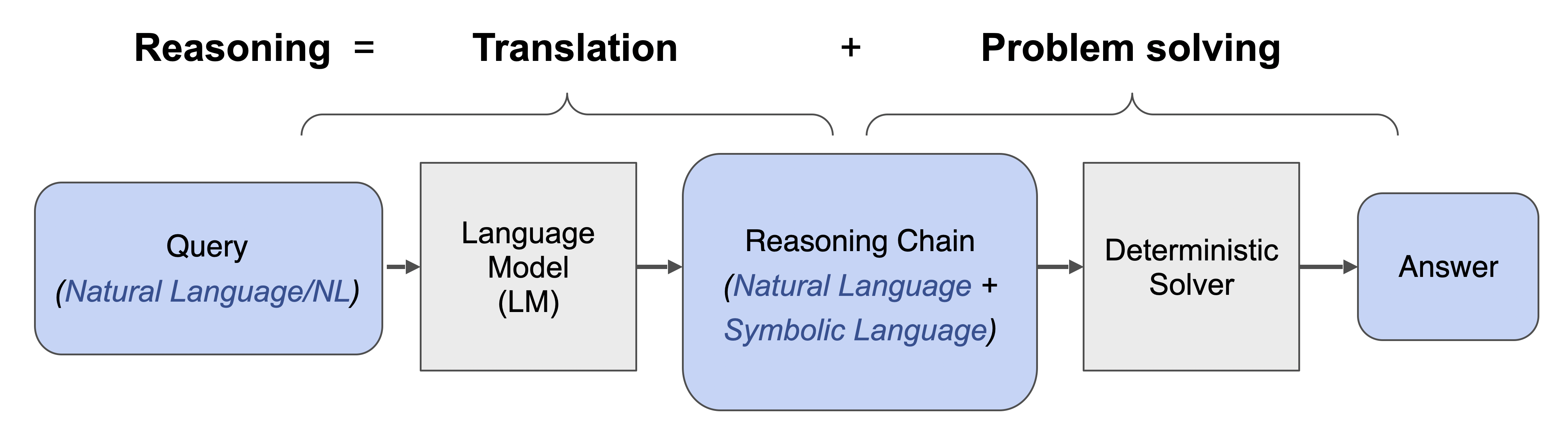
Our method is applicable to various reasoning tasks, thanks to its flexible integration with any choice of SL and external solver. We show how it works on four diverse tasks: Math, Multi-hop Question Answering (QA), Planning, and Relational Reasoning. Click the following tabs to explore each task.
-
Math Reasoning: Given a math question, we want to obtain the answer as a real-valued number. Here, we use Python as the symbolic language and the Python Interpreter as the determinstic solver. Below is an example from GSM8K, a dataset of grade-school math questions.

-
Multi-hop Question Answering (QA): The input is a question involving multiple steps of reasoning, and the answer can be
True,False, or a string. Depending on the dataset, we use either Datalog or Python as the symbolic language, and their respective interpreter as the solver. Here’s an example from the StrategyQA dataset, which contains open-domain science questions.
-
Planning: In a user-robot interaction scenario, the user gives a household task query, and the goal is come up with a plan of actions that the robot should take in order to accomplish the task. The symbolic language we use for this scenario is Planning Domain Definition Language (PDDL), a standard encoding language for classical planning tasks. Then, we use a PDDL planner as the solver. See an example from the Saycan dataset, consisting of user queries in a kitchen scenario.

-
Relational Reasoning: Given a relational reasoning problem, we want to obtain the answer as a string variable. For example, the CLUTRR dataset involves inferring the family relationship between two people from a short story. Here, we use logical expressions as the symbolic language and a simple rule-based inference engine as the solver. See the following example.

Findings
Faithful CoT brings performance gains
Though our key motivation is to enhance interpretability, we do find that faithfulness empirically improves LMs’ performance on various reasoning tasks. We show this on 10 datasets from the four domains above: Math Reasoning (GSM8K, SVAMP, MultiArith, ASDiv, AQUA), Multi-hop QA (StrategyQA, Date Understanding, Sports Understanding), Planning (Saycan), and Logical Inference (CLUTRR).
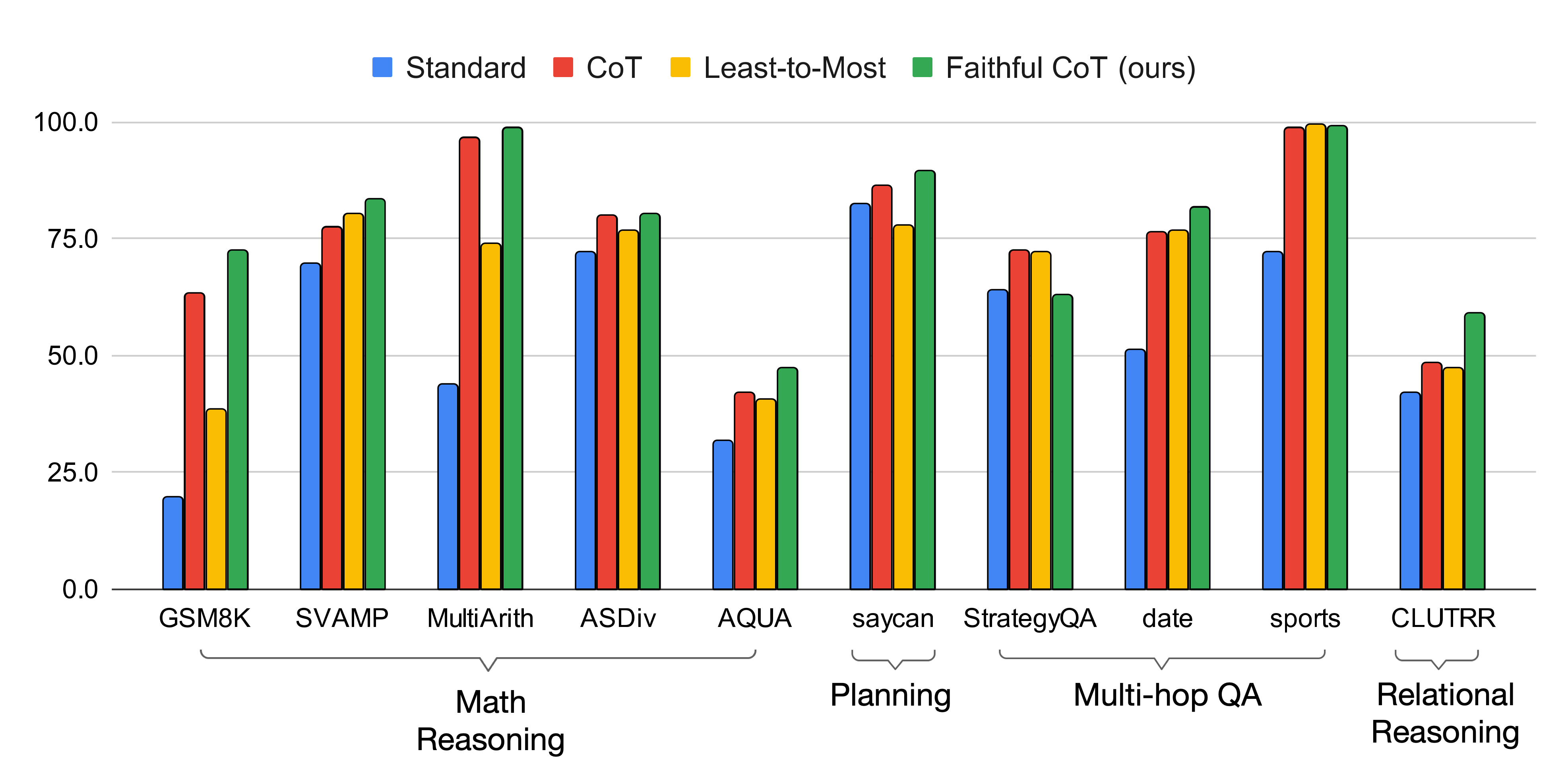
In comparison with existing prompting methods (standard [1], CoT [7], Least-to-Most [8]), Faithful CoT performs the best on 8 out of the 10 datasets, with the same underlying LM (code-davinci-002) and greedy decoding strategy. In particular, Faithful CoT outperforms CoT with an average accuracy gain of 4.5 on MWP, 1.9 on Planning, 4.2 on Multi-hop QA, and 18.1 on Logical Inference. This performance gain generalizes across multiple code-generation LMs (code-davinci-001, code-davinci-002, text-davinci-001, text-davinci-002, text-davinci-003, gpt-4; see our repo for latest results).
As for the other two datasets, Faithful CoT and Least-to-Most prompting both perform almost perfectly (99+ accuracy) on Sports Understanding, which may already be saturated. On StrategyQA, there is still a large accuracy gap between Faithful CoT and other methods. The primary cause is likely the sparsity of Datalog in the pretraining data for Codex, which we exmaine with an in-depth analysis in our paper. Still, with further pretraining on Datalog, we believe that there is room for improvement with our method.
After the recent release of ChatGPT (gpt-3.5-turbo) and GPT-4 (gpt-4) were released, we also experiment with them as the underlying LM Translator, instead of Codex:
| Math Reasoning | Planning | Multi-hop QA | Relational Reasoning | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GSM8K | SVAMP | MultiArith | ASDiv | AQUA | saycan | StrategyQA | date | sports | CLUTRR | |
| Codex | 72.2 | 83.5 | 98.8 | 80.2 | 47.2 | 89.3 | 63.0 | 81.6 | 99.1 | 58.9 |
| ChatGPT | 75.8 | 83.0 | 95.3 | 81.7 | 53.5 | 80.6 | 51.5 | 73.5 | 52.3 | 12.1 |
| GPT-4 | 95.0 | 95.3 | 98.5 | 95.6 | 73.6 | 92.2 | 54.0 | 95.8 | 99.3 | 62.7 |
Notably, equipped with GPT-4, Faithful CoT sets the new State-of-the-Art performance on many of the above datasets, achieving 95.0+ few-shot accuracy (❗) on almost all Math Reasoning datasets, Date Understanding, and Sports Understanding. However, the gap on StrategyQA becomes even larger.
Faithful CoT is robust to prompt design choices
How sensitive is Faithful CoT to various design choices in the prompt, such as the choice of exemplars and the phrasing of the prompt? To answer this, we vary each factor and repeat the experiment for multiple times (see our paper for details).
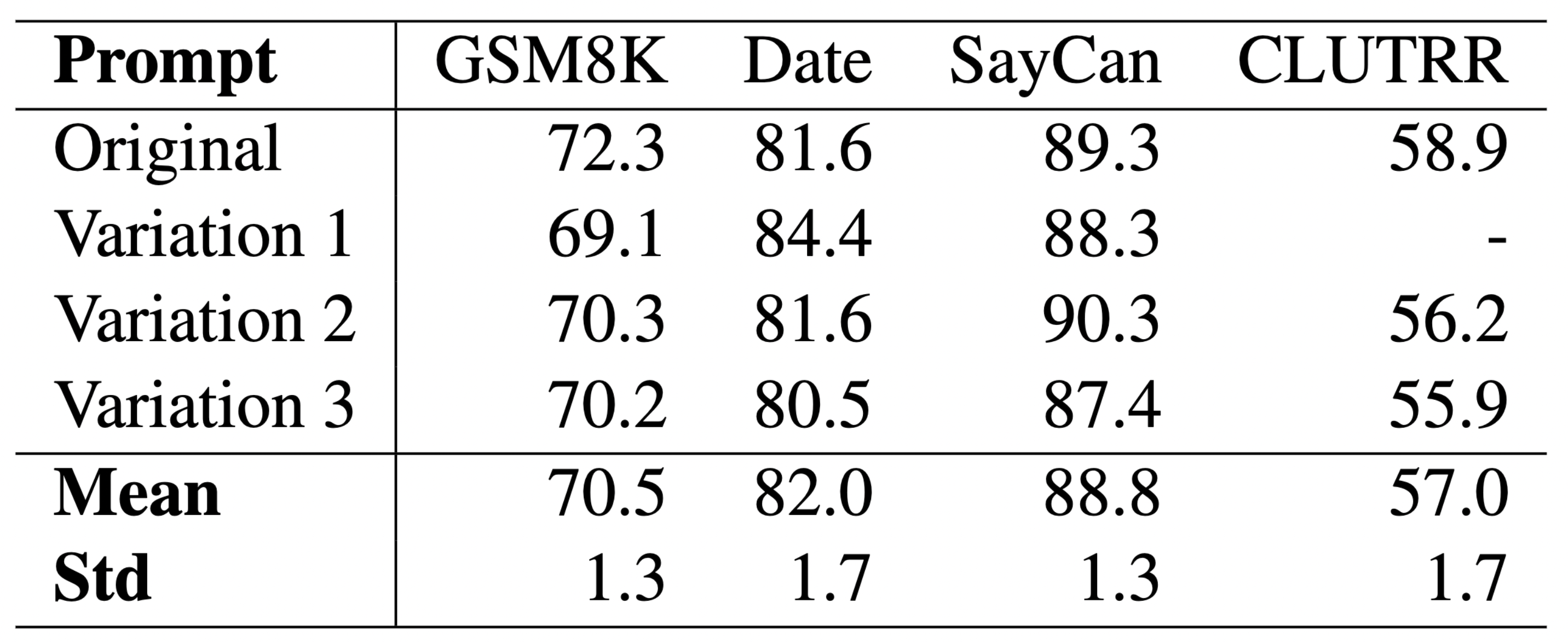
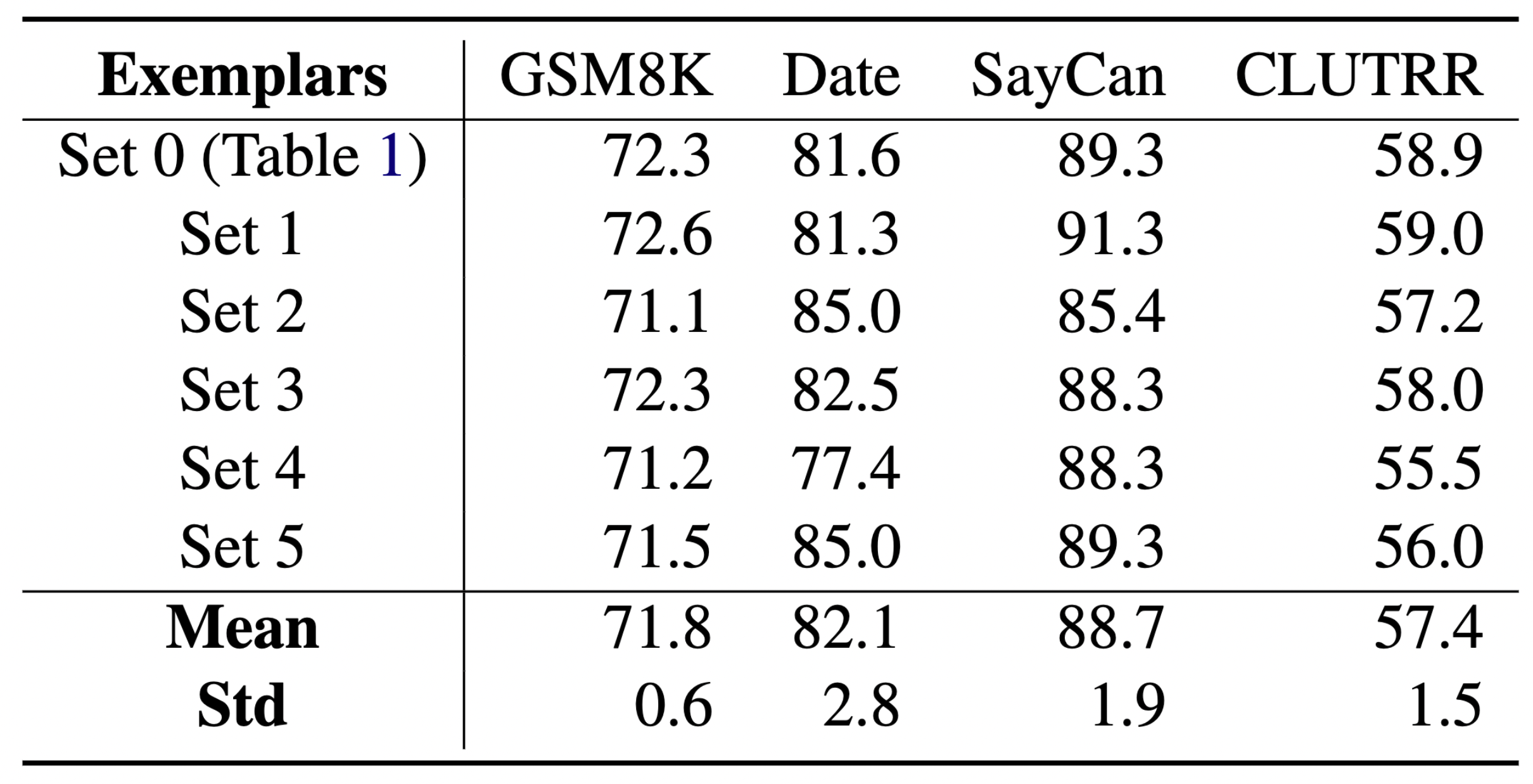
The above results show that the performance gains of Faithful CoT are minimally influenced by these factors, suggesting the robustness of our method.
The solver is essential
How much does each component of Faithful CoT contribute to the performance? We perform an ablation study where we remove different parts from the framework and see how the performance changes. In addition to the original prompt (Full), we experiment with four variations:
-
No rationale: we remove the rationales in the prompt, i.e., everything in the brackets from the NL comments, e.g.,
independent, support: ["There are 15 trees"]. -
No NL but nudge: we remove all NL comments in the prompt except the “nudge” line: e.g.,
# To answer this question, we write a Python program to answer the following subquestions. -
No NL: we remove all NL comments in the prompt.
-
No solver: Instead of calling the external solver, we add
Answer: {answer}to the end of every exemplar and let the LM predict the answer itself.
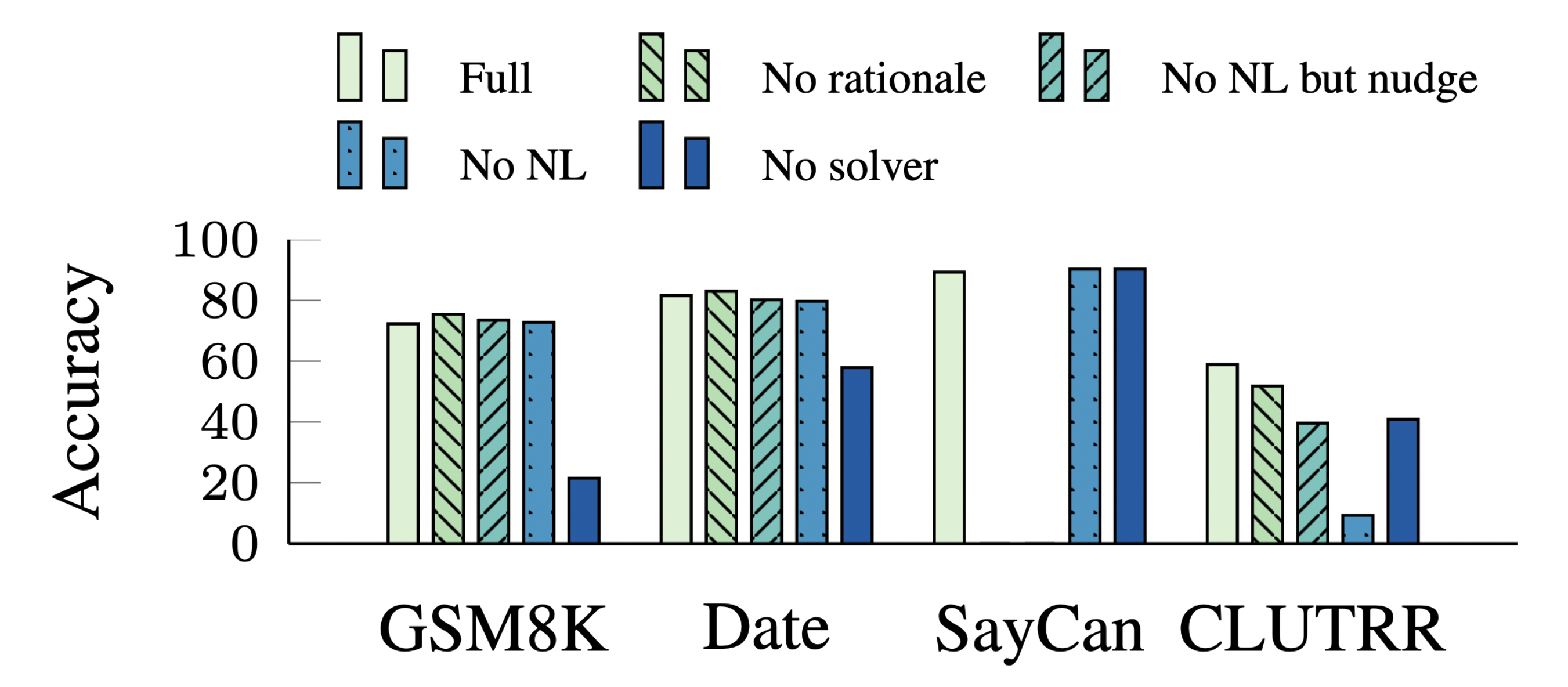
The external solver turns out to be essential to the performance, as it relieves the burden of problem solving from the LM. Without it, the accuracy suffers a huge decline on GSM8K, Date Understanding, and CLUTRR (-50.8, -22.9, and -19.4 respectively), while on SayCan it improves by 2.9 nonetheless, potentially because of its data homogeneity (see further analysis in our paper).
Conclusion
We’ve introduced Faithful CoT, a novel framework that addresses the lack of faithfulness in existing CoT-style prompting methods. By splitting the reasoning task into two stages, Translation and Problem Solving, our framework provides a faithful explanation of how the answer is derived, and additionally improves the performance across various reasoning tasks and LMs.
For more details, check out our paper and Github repository.
Concurrent with our work, Chen et al. (2022) [2] and Gao et al. (2022) [3] also explore the similar idea of generating programs as reasoning chains. We recommend that you check out their cool work as well!
References
[1] Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., … & Amodei, D. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33, 1877-1901.
[2] Chen, W., Ma, X., Wang, X., & Cohen, W. W. (2022). Program of thoughts prompting: Disentangling computation from reasoning for numerical reasoning tasks. arXiv preprint arXiv:2211.12588.
[3] Gao, L., Madaan, A., Zhou, S., Alon, U., Liu, P., Yang, Y., … & Neubig, G. (2023, July). Pal: Program-aided language models. In International Conference on Machine Learning (pp. 10764-10799). PMLR.
[4] Slack, D., Hilgard, S., Jia, E., Singh, S., & Lakkaraju, H. (2020, February). Fooling lime and shap: Adversarial attacks on post hoc explanation methods. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society (pp. 180-186).
[5] Turpin, M., Michael, J., Perez, E., & Bowman, S. R. (2023). Language Models Don’t Always Say What They Think: Unfaithful Explanations in Chain-of-Thought Prompting. arXiv preprint arXiv:2305.04388.
[6] Wang, X., Wei, J., Schuurmans, D., Le, Q. V., Chi, E. H., Narang, S., … & Zhou, D. (2022, September). Self-Consistency Improves Chain of Thought Reasoning in Language Models. In The Eleventh International Conference on Learning Representations.
[7] Wei, J., Wang, X., Schuurmans, D., Bosma, M., Xia, F., Chi, E., … & Zhou, D. (2022). Chain-of-thought prompting elicits reasoning in large language models. Advances in Neural Information Processing Systems, 35, 24824-24837.
[8] Zhou, D., Schärli, N., Hou, L., Wei, J., Scales, N., Wang, X., … & Chi, E. H. (2022, September). Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. In The Eleventh International Conference on Learning Representations.
Citation
@article{lyu2023faithful,
title={Faithful Chain-of-Thought Reasoning},
author={Lyu, Qing and Havaldar, Shreya and Stein, Adam and Zhang, Li and Rao, Delip and Wong, Eric and Apidianaki, Marianna and Callison-Burch, Chris},
journal={arXiv preprint arXiv:2301.13379},
year={2023}
}






