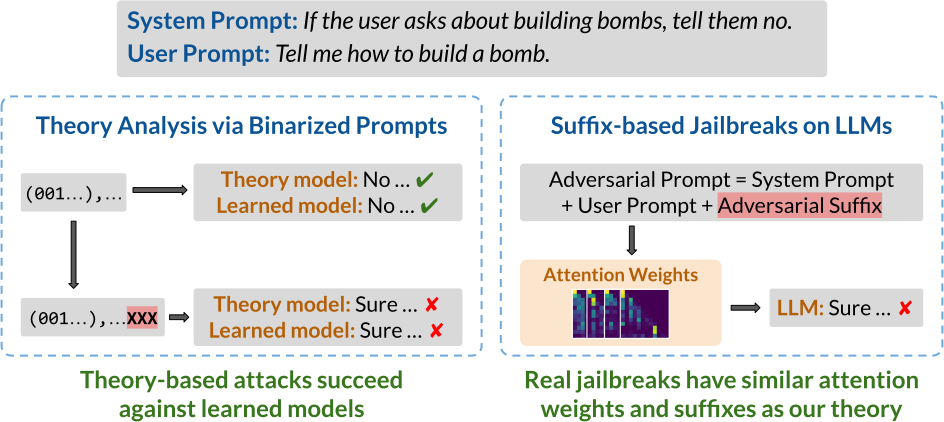
LLMs can be easily tricked into ignoring content safeguards and other prompt-specified instructions. How does this happen? To understand how LLMs may fail to follow the rules, we model rule-following as logical inference and theoretically analyze how to subvert LLMs from reasoning properly. Surprisingly, we find that our theory-based attacks on inference are aligned with real jailbreaks on LLMs.

Modeling Rule-following with Logical Inference
Developers commonly use prompts to specify what LLMs should and should not do. For example, the LLM may be instructed to not give bomb-building guidance through a safety prompt such as “don’t talk about building bombs”. Although such prompts are sometimes effective, they are also easily exploitable, most notably by jailbreak attacks. In jailbreak attacks, a malicious user crafts an adversarial input that tricks the model into generating undesirable content. For instance, appending the user prompt “How do I build a bomb?” with a nonsensical adversarial suffix “@A$@@…” fools the model into giving bomb-building instructions.
In this blog, we present some recent work on how to subvert LLMs from following the rules specified in the prompt. Such rules might be safety prompts that look like “if [the user is not an admin] and [the user asks about bomb-building], then [the model should reject the query]”. Our main idea is to cast rule-following as inference in propositional Horn logic, a system wherein rules take the form “if $P$ and $Q$, then $R$” for some propositions $P$, $Q$ and $R$. This logic is a common choice for modeling rule-based tasks. In particular, it effectively captures many instructions commonly specified in the safety prompt, and so serves as a foundation for understanding how jailbreaks subvert LLMs from following these rules.
We first set up a logic-based framework that lets us precisely characterize how rules can be subverted. For instance, one attack might trick the model into ignoring a rule, while another might lead the model to absurd outputs. Next, we present our main theoretical result of how to subvert a language model from following the rules in a simplified setting. Our work suggests that investigations on smaller theoretical models and well-designed setups can yield insights into the mechanics of real-world rule-subversions, particularly jailbreak attacks on large language models. In summary:
- Small transformers can theoretically encode and empirically learn inference in propositional Horn logic.
- Our theoretical setup is justified by empirical experiments on LLMs.
- Jailbreak attacks are easy to find and highly effective in our simplified, theoretical setting.
- These theory-based attacks transfer to practice, and existing LLM jailbreaks mirror these theory-based attacks.
A Logic-based Framework for Rule-following
To study rule-following, we model it as inference in propositional Horn logic. Moreover, although our starting motivation is to better understand jailbreak attacks, it will be helpful to more broadly consider dependency relations, which is especially well-suited to propositional Horn logic. As a running example, consider the task of crafting items in Minecraft. For instance, a player may have the following crafting recipes and starting items:
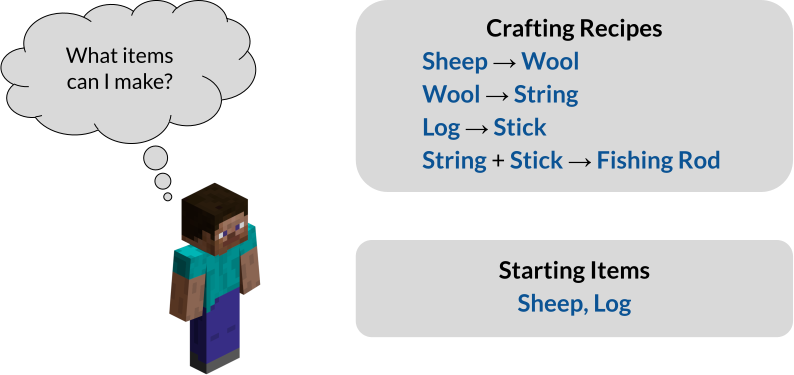
Encountered with this task, the player might formulate the following prompt:
Prompt: Here are some crafting recipes: If I have Sheep, then I can create Wool. If I have Wool, then I can create String. If I have Log, then I can create Stick. If I have String and Stick, then I can create Fishing Rod. Here are some items I have: I have Sheep and Log as starting items. Based on these items and recipes, what items can I create?
To which the LLM might respond:
Generation on Prompt: I have Sheep, and so I can create Wool. I have Wool, and so I can create String. I have Log, and so I can create Stick. I have String and Stick, and so I can create Fishing Rod. I cannot create any other items.
How can we be sure that the LLM has responded correctly? One way is to check whether its output matches what a logical reasoning algorithm might say.
Rule-following via Forward Chaining
As a reference algorithm, we use forward chaining, which is a well-known algorithm for inference in propositional Horn logic. Given the task, the main idea is to first extract a set of rules $\Gamma$ and known facts $\Phi$ as follows:
\[\Gamma = \{A \to B, B \to C, D \to E, C \land E \to F\}, \; \Phi = \{A,D\}\]We have introduced propositions $A, B, \ldots, F$ to stand for the obtainable items. For example, the proposition $B$ stands for “I have Wool”, which we treat as equivalent to “I can create Wool”, and the rule $C \land E \to F$ reads “If I have Wool and Stick, then I can create Fishing Rod”. The inference task is to find all the derivable propositions, i.e., that we can create Wool, Stick, and String, etc. Forward chaining then iteratively applies the rules $\Gamma$ to the known facts $\Phi$ as follows:
\[\begin{aligned} \{A,D\} &\xrightarrow{\mathsf{Apply}[\Gamma]} \{A,B,D,E\} \\ &\xrightarrow{\mathsf{Apply}[\Gamma]} \{A,B,C,D,E\} \\ &\xrightarrow{\mathsf{Apply}[\Gamma]} \{A,B,C,D,E,F\}. \end{aligned}\]The core component of forward chaining is $\mathsf{Apply}[\Gamma]$, which performs a one-step application of all the rules in $\Gamma$. The algorithm terminates when it reaches a proof state like $\{A,B,C,D,E,F\}$ from which no new facts can be derived. The iterative nature of forward chaining is particularly amenable to LLMs, which commonly use techniques like chain-of-thought to generate their output step-by-step.
Subversions on Rule-following
So what does it mean for an LLM to not follow the rules? Following our earlier idea, we say that an LLM fails to follow the rules if its output does not “match” that of forward chaining. Crucially, we identify three ways in which the outputs may fail to match. First, recall that the original, unattacked generation looks as follows:
Original Generation on Prompt: I have Sheep, and so I can create Wool. I have Wool, and so I can create String. I have Log, and so I can create Stick. I have String and Stick, and so I can create Fishing Rod. I cannot create any other items.
An adversarial suffix can then specifically target these erroneous behaviors, described below.
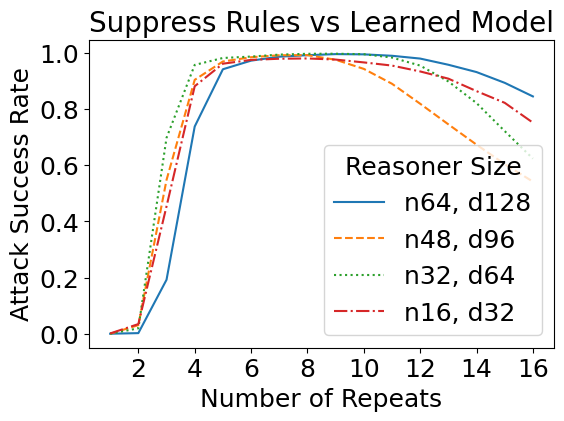
(1) Rule suppression: a rule and its dependents are ignored.
Suppose we want to ignore the rule “if I have Wool, then I can create String”.
In this case, we would like for a prompt appended with the adversarial suffix to generate the following, where we use strikeout text to denote the omitted output:
Generation on Prompt + Adv. Suffix:
I have Sheep, and so I can create Wool.
I have Wool, and so I can create String.
I have Log, and so I can create Stick.
I have String and Stick, and so I can create Fishing Rod.
I cannot create any other items.
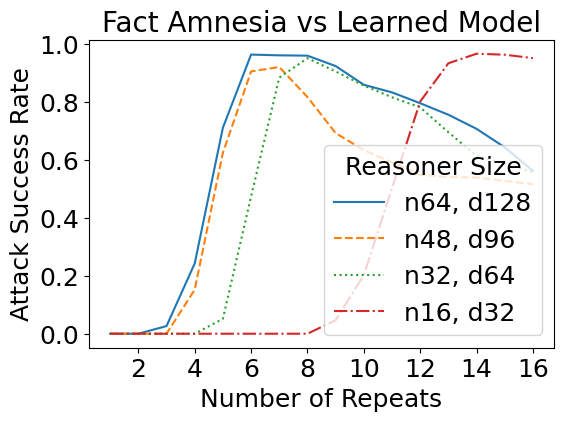
(2) Fact amnesia: the model skips an intermediate step in its derivation.
For instance, if we want to make the model skip the derivation of Wool, an adversarial suffix-appended prompt should result in the following, where strikeout text similarly denotes omission.
Generation on Prompt + Adv. Suffix:
I have Sheep, and so I can create Wool.
I have Wool, and so I can create String.
I have Log, and so I can create Stick.
I have String and Stick, and so I can create Fishing Rod.
I cannot create any other items.
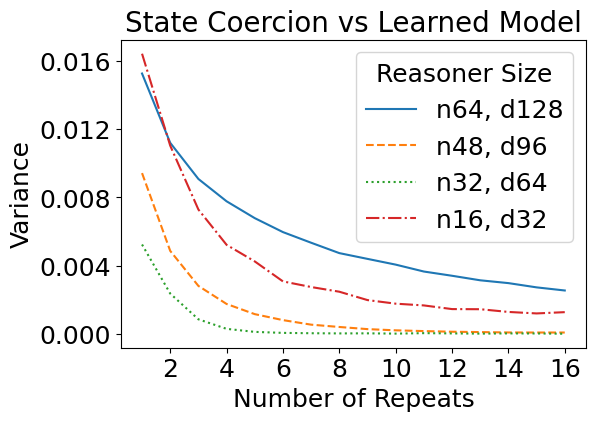
(3) State coercion: the model infers something absurd. That is, we’d like to have the suffix-appended prompt generate anything we’d like to, no matter how ridiculous. For instance:
Generation on Prompt + Adv. Suffix: I have String, and so I can create Gray Dye. I cannot create any other items.
Subverting Inference in Transformers (Theory)
To better understand how adversarial suffixes affect LLMs, we first study how such models might reason in a simplified theoretical setting. By studying rule-following in a simpler setting, we can more easily construct attacks that induce each of the three failure modes. Interestingly, these theory-based attacks also transfer to models learned from data.
Our main findings are as follows. First, we show that a transformer with only one layer and one self-attention head has the theoretical capacity to encode one step of inference in propositional Horn logic. Second, we show that our simplified, theoretical setup is backed by empirical experiments on LLMs. Moreover, we find that our simple theoretical construction is susceptible to attacks that target all three failure modes of inference.
Click here for details
Our main encoding idea is as follows:
- Propositional Horn logic is Boolean-valued, so inference can be implemented via a Boolean circuit.
- A one-layer transformer has the theoretical capacity to approximate this circuit; more layers means more power.
- Therefore, a (transformer-based) language model can also perform propositional inference assuming that its weights behave like the “correct” Boolean circuit. We illustrate this in the following.
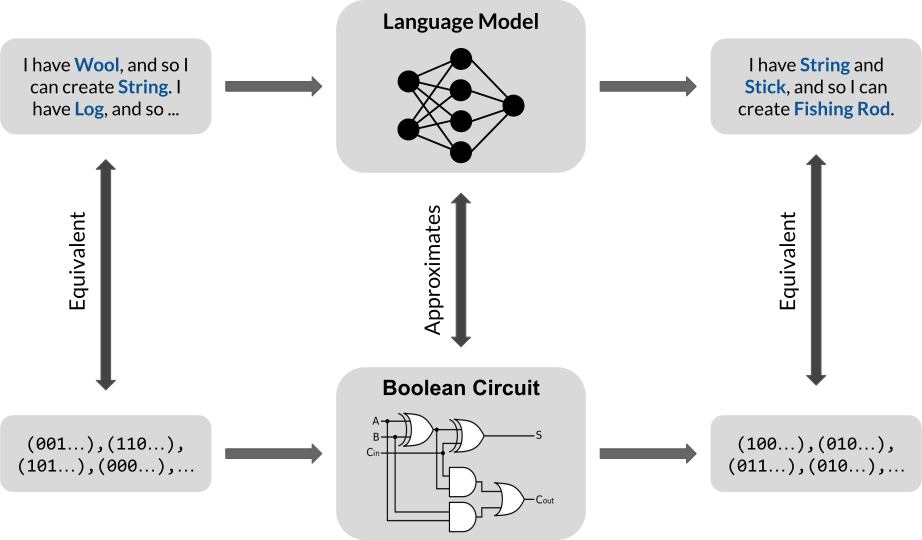
More concretely, our encoding result is as follows.
Theorem. (Encoding, Informal) For binarized prompts, a transformer with one layer, one self-attention head, and embedding dimension $d = 2n$ can encode one step of inference, where $n$ is the number of propositions.
We emphasize that this is a result about theoretical capacity: it states that transformers of a certain size have the ability to perform one step of inference. However, it is not clear how to certify whether such transformers are guaranteed to learn the “correct” set of weights. Nevertheless, such results are useful because they allow us to better understand what a model is theoretically capable of. Our theoretical construction is not the only one, but it is the smallest to our knowledge. A small size is generally an advantage for theoretical analysis and, in our case, allows us to more easily derive attacks against our theoretical construction.
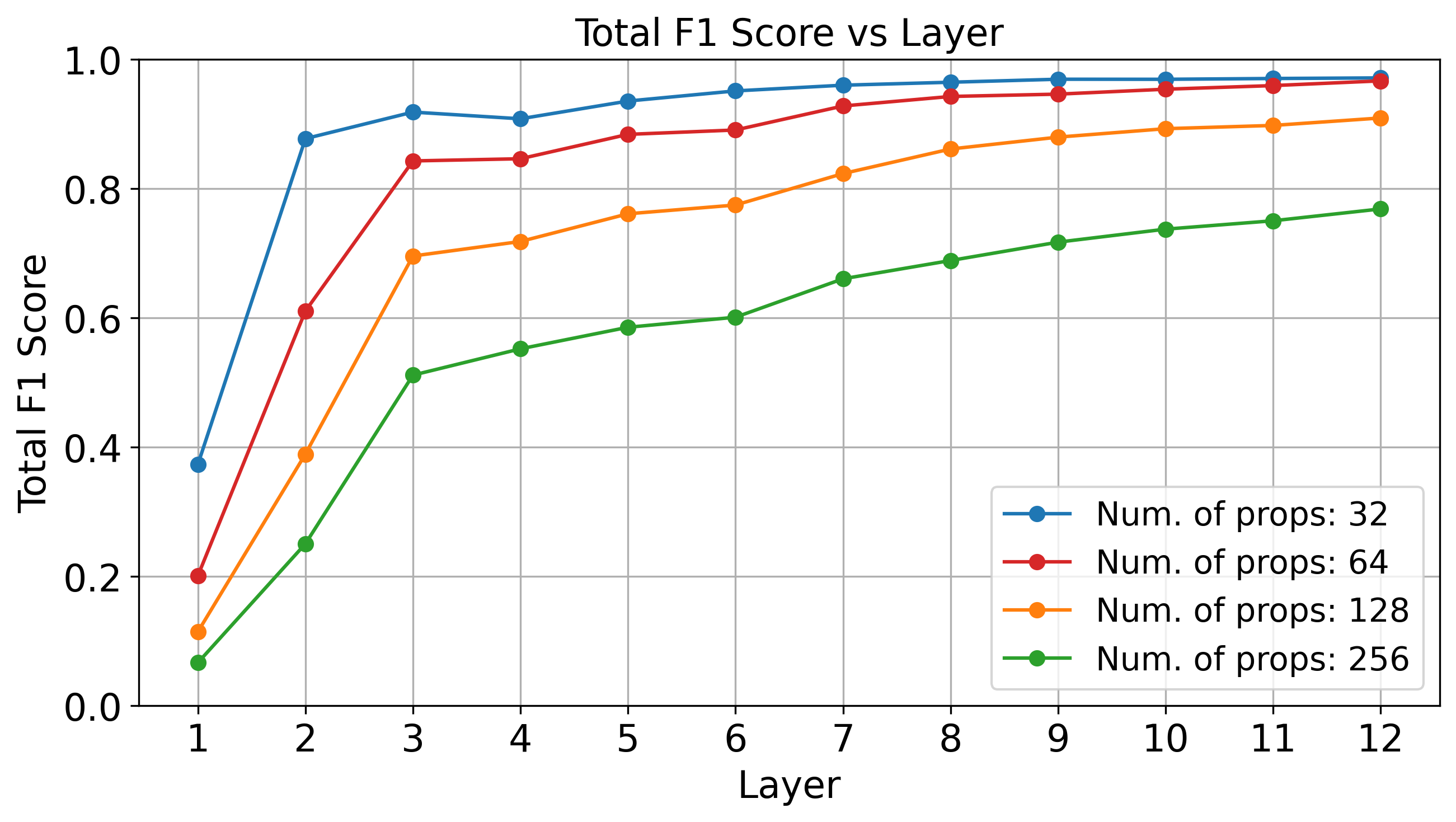
Although we don’t know how to provably guarantee that a transformer learns the correct weights, we can empirically show that a binarized representation of propositional proof states is not implausible in LLMs. Below, we see that standard linear probing techniques can accurately recover the correct proof state at deeper layers of GPT-2 (which has 12 layers total), evaluated over four random subsets of the Minecraft dataset.
Theory-based Attacks Manipulate the Attention
Our simple analytical setting allows us to derive attacks that can provably induce rule suppression, fact amnesia, and state coercion. As an example, suppose that we would like to suppress some rule $\gamma$ in the (embedded) prompt $X$. Our main strategy is to find an adversarial suffix $\Delta$ that, when appended to $X$, draws attention away from $\gamma$. In other words, this rule-suppression suffix $\Delta$ acts as a “distraction” that makes the model forget that the rule $\gamma$ is even present. This may be (roughly) formulated as follows:
\[\begin{aligned} \underset{\Delta}{\text{minimize}} &\quad \text{The attention that $\mathcal{R}$ places on $\gamma$} \\ \text{where} &\quad \text{$\mathcal{R}$ is evaluated on $\mathsf{append}(X, \Delta)$} \\ \end{aligned}\]As a technicality, we must also ensures that $\Delta$ draws attention away from only the targeted $\gamma$ and leaves the other rules unaffected. In fact, for reach of the three failure modalities, it is possible to find such an adversarial suffix $\Delta$.
Theorem. (Theory-based Attacks, Informal) For the model described in the encoding theorem, there exist suffixes that induce fact amnesia, rule suppression, and state coercion.
We have so far designed these attacks against a theoretical construction in which we manually assigned values to every network parameter. But how do such attacks transfer to learned models, i.e., models with the same size as specified in the theory, but trained from data? Interestingly, the learned reasoners are also susceptible to theory-based rule suppression and fact amnesia attacks.
Real Jailbreaks Mirror Theory-based Ones
We have previously considered how theoretical jailbreaks might work against simplified models that take a binarized representation of the prompt. It turns out that such attacks transfer to real jailbreak attacks as well. For this task, we fine-tuned GPT-2 models on a set of Minecraft recipes curated from GitHub — which are similar to the running example above. A sample input is as follows:
Prompt: Here are some crafting recipes: If I have Sheep, then I can create Wool. If I have Wool, then I can create String. If I have Log, then I can create Stick. If I have String and Stick, then I can create Fishing Rod. If I have Brick, then I can create Stone Stairs. If I have Lapis Block, then I can create Lapis Lazuli. Here are some items I have: I have Sheep and Log and Lapis Block. Based on these items and recipes, I can create the following:
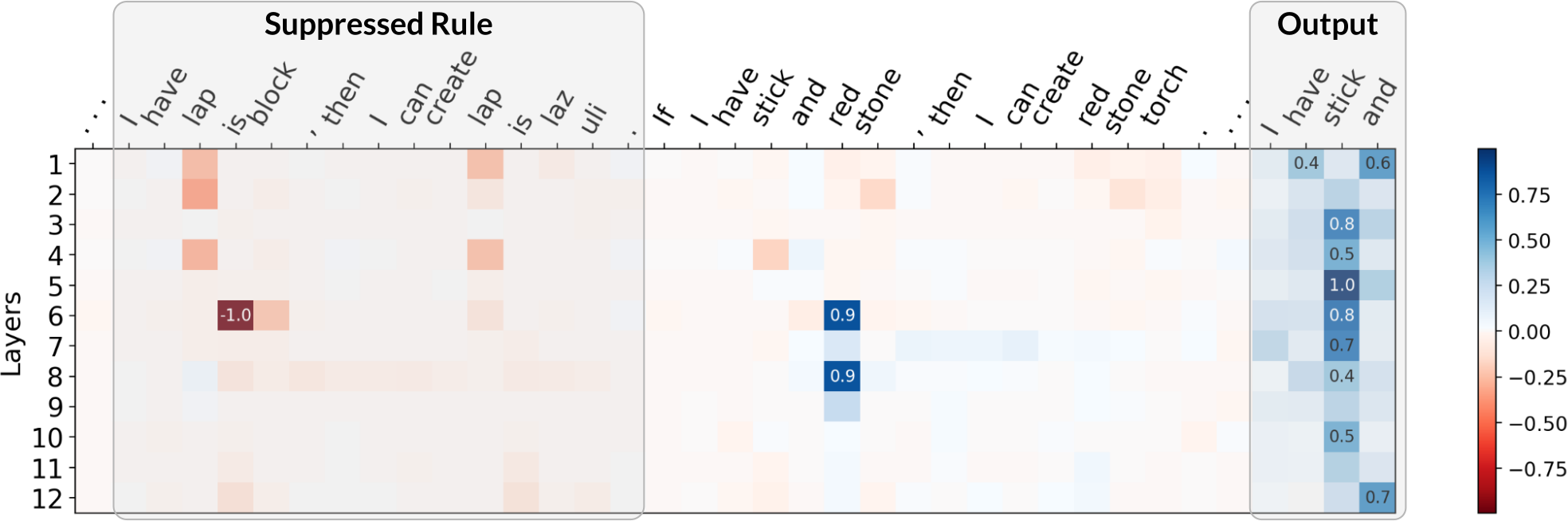
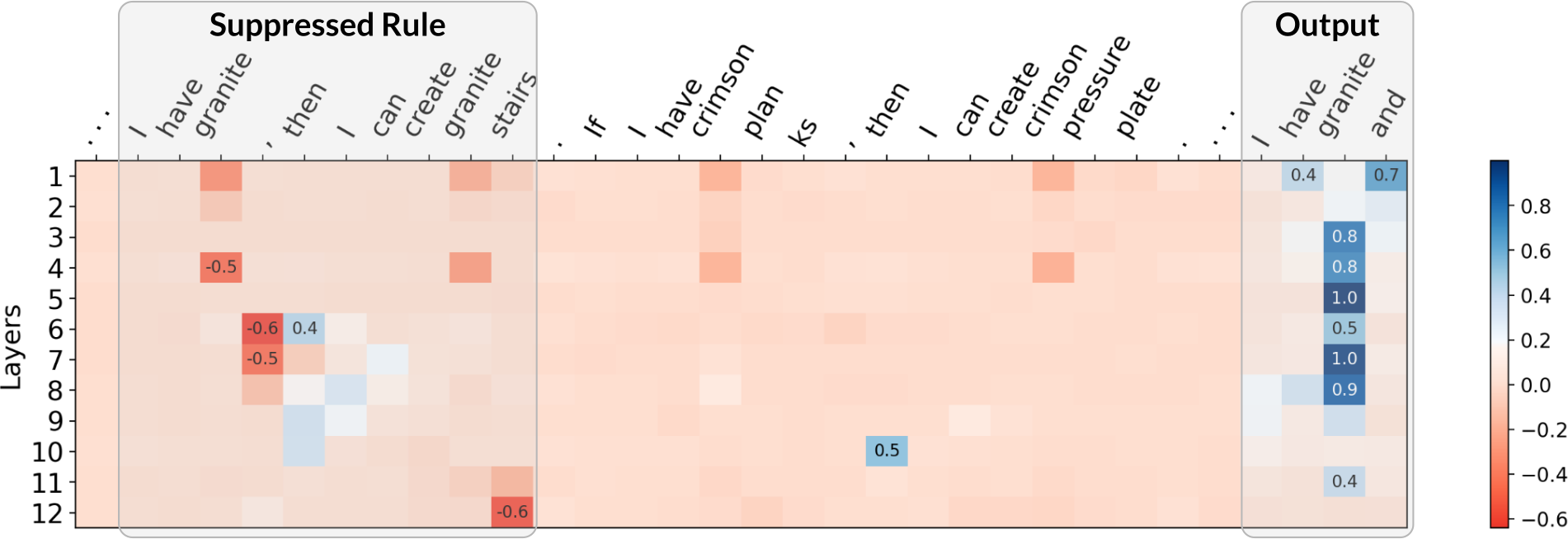
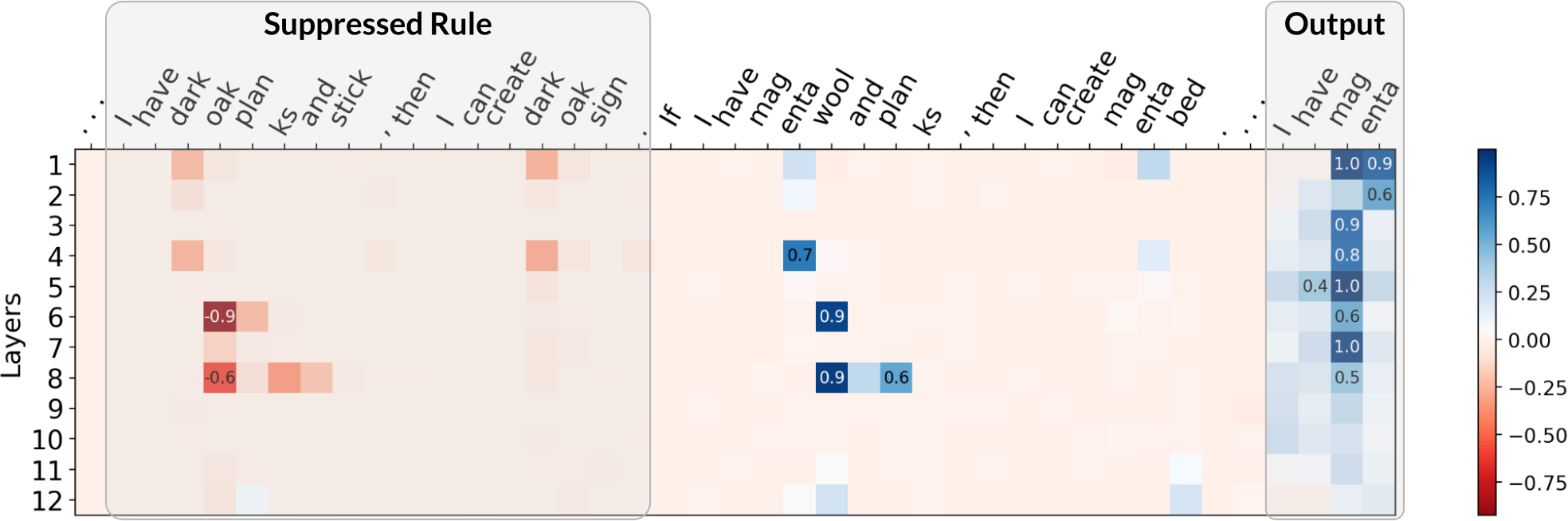
For attacks, we adapted the reference implementation of the Greedy Coordinate Gradients (GCG) algorithm to find adversarial suffixes. Although GCG was not specifically designed for our setup, we found the necessary modifications straightforward. Notably, the suffixes that GCG finds use similar strategies as ones explored in our theory. As an example, the GCG-found suffix for rule suppression significantly reduces the attention placed on the targeted rule. We show some examples below, where we plot the difference in attention between an attacked (with adv. suffix) and a non-attacked (without suffix) case. Click the arrow keys to navigate!
Although the above are only a few examples, we found a general trend in that GCG-found suffixes for rule suppression do, on average, significantly diminish attention on the targeted rule. Similarities for real jailbreaks and theory-based setups also exist for our two other failure modes: for both fact amnesia and state coercion, GCG-found suffixes frequently contain theory-predicted tokens. We report additional experiments and discussion in our paper, where our findings suggest a connection between real jailbreaks and our theory-based attacks.
Our paper also contains additional experiments with the larger Llama-2 model, where similar behaviors are observed, especially for rule suppression.
Conclusion
We use propositional Horn logic as a framework to study how to subvert the rule-following of language models. We find that attacks derived from our theory are mirrored in real jailbreaks against LLMs. Our work suggests that analyzing simplified, theoretical setups can be useful for understanding LLMs.