

Explanations for machine learning need interpretable features, but current methods fall short of discovering them. Intuitively, interpretable features should align with domain-specific expert knowledge. Can we measure the interpretability of such features and in turn automatically find them? In this blog post, we delve into our joint work with domain experts in creating the FIX benchmark, which directly evaluates the interpretability of features in real world settings, ranging from psychology to cosmology.
Machine learning models are increasingly used in domains like healthcare, law, governance, science, education, and finance. Although state-of-the-art models attain good performance, domain experts rarely trust them because the underlying algorithms are black-box. This lack of transparency is a liability in critical fields such as healthcare and law. In these domains, experts need explanations to ensure the safe and effective use of machine learning.
One popular approach towards transparent models is to explain model behaviors in terms of the input features, i.e. the pixels of an image or the tokens of a prompt. However, feature-based explanation methods often do not produce interpretable explanations. One major challenge is that feature-based explanations commonly assume that the given features are already interpretable to the user, but this is typically only true for low-dimensional data. With high-dimensional data like images and documents, features at the granularity of pixels and tokens may lack enough semantically meaningful information to be understood even by experts. Moreover, the features relevant for an explanation are often domain-dependent, as experts of different domains will care about different features. These factors limit the usability of popular, general-purpose feature-based explanation techniques on high-dimensional data.
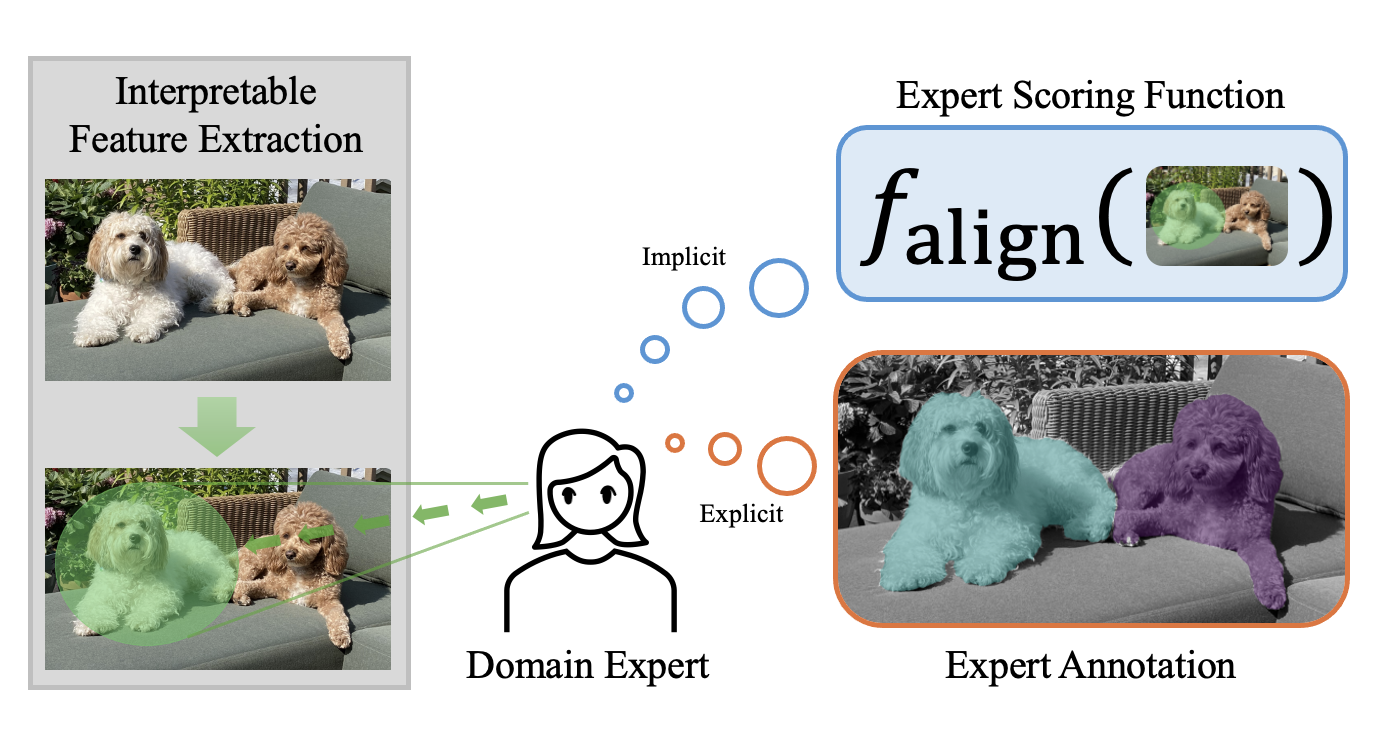
Instead of individual features, users often understand high-dimensional data in terms of semantic collections of low-level features, such as regions of an image or phrases in a document. In the figure above, a pixel as a feature would not be very informative, but rather the pixels that make up a dog in the image would make more sense to a user. Furthermore, for a feature to be useful, it should align with the intuition of domain experts in the field. Therefore, an interpretable feature for high-dimensional data should satisfy the following properties:
We refer to features that satisfy these criteria as expert features. In other words, an expert feature is a high-level feature that experts in the domain find semantically meaningful and useful. This benchmark thus aims to provide a platform for researching the following question:
Can we automatically discover expert features that align with domain knowledge?
Towards this goal, we present FIX, a benchmark for measuring the interpretability of features with respect to expert knowledge. To develop this benchmark, we worked closely with with domain experts, spanning gallbladder surgeons to supernova cosmologists, to define criteria for interpretability of features in each domain.
An overview of FIX is shown in the following table below. The benchmark consists of 6 different real-world settings spanning cosmology, psychology and medicine, and covers 3 different data modalities (image, text, and time series). Each setting’s dataset consists of classic inputs and outputs for prediction, as well as the criteria that experts consider to reflect their desired features (i.e. expert features). Despite the breadth of domains, FIX generalizes all of these different settings into a single framework with a unified metric that measures a feature’s alignment with expert knowledge. The goal of the benchmark is to advance the development of general purpose feature extractors that can extract expert feature across all diverse FIX settings.

As an example, in cholecystectomy (gallbladder removal surgery), surgeons consider vital organs and structures (such as the liver, gallbladder, hepatocystic triangle) when making decisions in the operating room, such as identifying regions (i.e. the so-called “critical view of safety”) that are safe to operate on.
[Warning!] Clicking on a blurred image below will show the unblurred color version of the image. This depicts the actual surgery which can be graphic in nature. Please click at your own discretion.


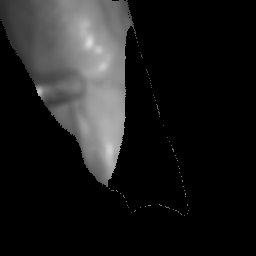
Therefore, image segments corresponding to organs are expert features. Specifically, we call this an explicit expert feature: such features can be explicitly labeled via mask annotations that show each organ (i.e. one mask per organ).
In FIX, the goal is to propose groups of features that align well with expert features. How do we measure this alignment? Let $\hat G$ also be a set of masks that correspond to proposed groups of features, called the candidate features.
To evaluate the alignment of a set of candidate features $\hat G$ for an example $x$, we define the following general-purpose FIXScore:
where \(\hat{G}[i] = \{\hat{g} : \text{group \(\hat{g}\) includes feature \(i\)}\}\) is the set of all groups containing the $i$th feature, and $\mathsf{ExpertAlign}(\hat g, x)$ measures how well a proposed feature $\hat g$ aligns with the experts’ judgment. In other words, the $\mathsf{FIXScore}$ computes an average alignment score for each individual low-level feature based on the groups that contain it, and summarizes the result as an average over all low-level features. This design prevents near-duplicate groups from inflating the score, while rewarding the proposal of new, different groups.
To adapt the FIX score to a specific domain, it suffices to define the $\mathsf{ExpertAlign}$ score for a single group. In the Cholecystectomy setting, we have existing ground truth annotations $G^\star$ from experts. These annotations allow us to define an explicit alignment score. Specifically, let $G^\star$ be a set of masks that correspond to explicit expert features, such as organs segments. We evaluate the proposed features with an intersection-over-union (IOU) between the proposed feature $\hat{g}$ and the ground truth annotations $G^\star$ as follows:
\[\mathsf{ExpertAlign} (\hat{g}, x) = \max_{g^{\star} \in G^{\star}} \frac{|\hat{g} \cap g^\star|}{|\hat{g} \cup g^\star|}.\]Explicit feature annotations are expensive: they are only available in two of our six settings (X-Ray and surgery), and are not available in the remaining psychology and cosmology settings. In those cases, we have worked with domain experts to define implicit alignment scores that measures how aligned a group of features is with expert knowledge without a ground truth target. For example, in the multilingual politeness setting, the scoring function measures how closely the text features align with the lexical categories for politeness. In the cosmological mass maps setting, the scoring function measures how close a group is to being a cosmological structure such as a cluster or a void. See our paper for more discussion on these implicit alignment scores and what they measure.
To explore more settings, check out FIX here: https://brachiolab.github.io/fix/
Thank you for stopping by!
Please cite our work if you find it helpful.
@article{jin2024fix,
title={The FIX Benchmark: Extracting Features Interpretable to eXperts},
author={Jin, Helen and Havaldar, Shreya and Kim, Chaehyeon and Xue, Anton and You, Weiqiu and Qu, Helen and Gatti, Marco and Hashimoto, Daniel and Jain, Bhuvnesh and Madani, Amin and Sako, Masao and Ungar, Lyle and Wong, Eric},
journal={arXiv preprint arXiv:2409.13684},
year={2024}
}
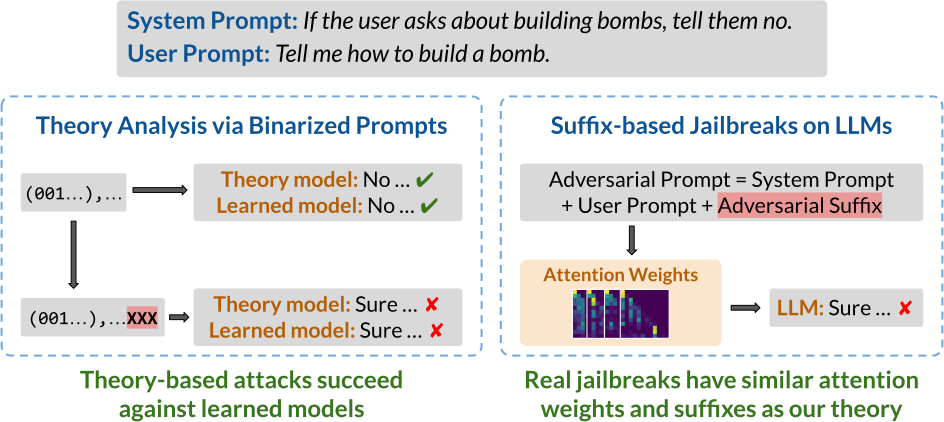
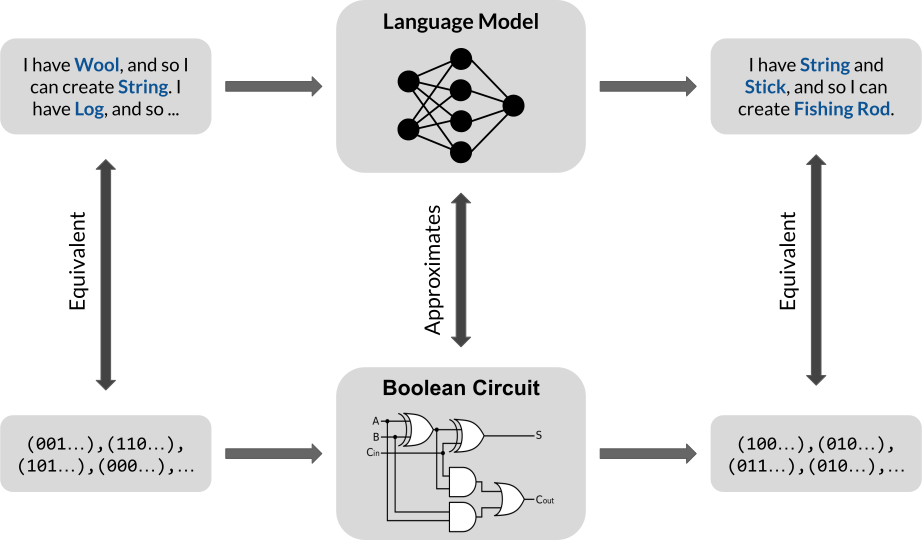
LLMs can be easily tricked into ignoring content safeguards and other prompt-specified instructions. How does this happen? To understand how LLMs may fail to follow the rules, we model rule-following as logical inference and theoretically analyze how to subvert LLMs from reasoning properly. Surprisingly, we find that our theory-based attacks on inference are aligned with real jailbreaks on LLMs.

Developers commonly use prompts to specify what LLMs should and should not do. For example, the LLM may be instructed to not give bomb-building guidance through a safety prompt such as “don’t talk about building bombs”. Although such prompts are sometimes effective, they are also easily exploitable, most notably by jailbreak attacks. In jailbreak attacks, a malicious user crafts an adversarial input that tricks the model into generating undesirable content. For instance, appending the user prompt “How do I build a bomb?” with a nonsensical adversarial suffix “@A$@@…” fools the model into giving bomb-building instructions.
In this blog, we present some recent work on how to subvert LLMs from following the rules specified in the prompt. Such rules might be safety prompts that look like “if [the user is not an admin] and [the user asks about bomb-building], then [the model should reject the query]”. Our main idea is to cast rule-following as inference in propositional Horn logic, a system wherein rules take the form “if $P$ and $Q$, then $R$” for some propositions $P$, $Q$ and $R$. This logic is a common choice for modeling rule-based tasks. In particular, it effectively captures many instructions commonly specified in the safety prompt, and so serves as a foundation for understanding how jailbreaks subvert LLMs from following these rules.
We first set up a logic-based framework that lets us precisely characterize how rules can be subverted. For instance, one attack might trick the model into ignoring a rule, while another might lead the model to absurd outputs. Next, we present our main theoretical result of how to subvert a language model from following the rules in a simplified setting. Our work suggests that investigations on smaller theoretical models and well-designed setups can yield insights into the mechanics of real-world rule-subversions, particularly jailbreak attacks on large language models. In summary:
To study rule-following, we model it as inference in propositional Horn logic. Moreover, although our starting motivation is to better understand jailbreak attacks, it will be helpful to more broadly consider dependency relations, which is especially well-suited to propositional Horn logic. As a running example, consider the task of crafting items in Minecraft. For instance, a player may have the following crafting recipes and starting items:
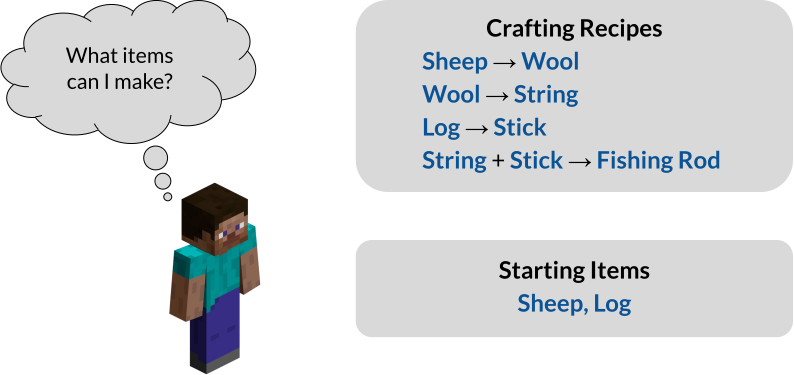
Encountered with this task, the player might formulate the following prompt:
Prompt: Here are some crafting recipes: If I have Sheep, then I can create Wool. If I have Wool, then I can create String. If I have Log, then I can create Stick. If I have String and Stick, then I can create Fishing Rod. Here are some items I have: I have Sheep and Log as starting items. Based on these items and recipes, what items can I create?
To which the LLM might respond:
Generation on Prompt: I have Sheep, and so I can create Wool. I have Wool, and so I can create String. I have Log, and so I can create Stick. I have String and Stick, and so I can create Fishing Rod. I cannot create any other items.
How can we be sure that the LLM has responded correctly? One way is to check whether its output matches what a logical reasoning algorithm might say.
As a reference algorithm, we use forward chaining, which is a well-known algorithm for inference in propositional Horn logic. Given the task, the main idea is to first extract a set of rules $\Gamma$ and known facts $\Phi$ as follows:
\[\Gamma = \{A \to B, B \to C, D \to E, C \land E \to F\}, \; \Phi = \{A,D\}\]We have introduced propositions $A, B, \ldots, F$ to stand for the obtainable items. For example, the proposition $B$ stands for “I have Wool”, which we treat as equivalent to “I can create Wool”, and the rule $C \land E \to F$ reads “If I have Wool and Stick, then I can create Fishing Rod”. The inference task is to find all the derivable propositions, i.e., that we can create Wool, Stick, and String, etc. Forward chaining then iteratively applies the rules $\Gamma$ to the known facts $\Phi$ as follows:
\[\begin{aligned} \{A,D\} &\xrightarrow{\mathsf{Apply}[\Gamma]} \{A,B,D,E\} \\ &\xrightarrow{\mathsf{Apply}[\Gamma]} \{A,B,C,D,E\} \\ &\xrightarrow{\mathsf{Apply}[\Gamma]} \{A,B,C,D,E,F\}. \end{aligned}\]The core component of forward chaining is $\mathsf{Apply}[\Gamma]$, which performs a one-step application of all the rules in $\Gamma$. The algorithm terminates when it reaches a proof state like $\{A,B,C,D,E,F\}$ from which no new facts can be derived. The iterative nature of forward chaining is particularly amenable to LLMs, which commonly use techniques like chain-of-thought to generate their output step-by-step.
So what does it mean for an LLM to not follow the rules? Following our earlier idea, we say that an LLM fails to follow the rules if its output does not “match” that of forward chaining. Crucially, we identify three ways in which the outputs may fail to match. First, recall that the original, unattacked generation looks as follows:
Original Generation on Prompt: I have Sheep, and so I can create Wool. I have Wool, and so I can create String. I have Log, and so I can create Stick. I have String and Stick, and so I can create Fishing Rod. I cannot create any other items.
An adversarial suffix can then specifically target these erroneous behaviors, described below.
(1) Rule suppression: a rule and its dependents are ignored.
Suppose we want to ignore the rule “if I have Wool, then I can create String”.
In this case, we would like for a prompt appended with the adversarial suffix to generate the following, where we use strikeout text to denote the omitted output:
Generation on Prompt + Adv. Suffix:
I have Sheep, and so I can create Wool.
I have Wool, and so I can create String.
I have Log, and so I can create Stick.
I have String and Stick, and so I can create Fishing Rod.
I cannot create any other items.
(2) Fact amnesia: the model skips an intermediate step in its derivation.
For instance, if we want to make the model skip the derivation of Wool, an adversarial suffix-appended prompt should result in the following, where strikeout text similarly denotes omission.
Generation on Prompt + Adv. Suffix:
I have Sheep, and so I can create Wool.
I have Wool, and so I can create String.
I have Log, and so I can create Stick.
I have String and Stick, and so I can create Fishing Rod.
I cannot create any other items.
(3) State coercion: the model infers something absurd. That is, we’d like to have the suffix-appended prompt generate anything we’d like to, no matter how ridiculous. For instance:
Generation on Prompt + Adv. Suffix: I have String, and so I can create Gray Dye. I cannot create any other items.
To better understand how adversarial suffixes affect LLMs, we first study how such models might reason in a simplified theoretical setting. By studying rule-following in a simpler setting, we can more easily construct attacks that induce each of the three failure modes. Interestingly, these theory-based attacks also transfer to models learned from data.
Our main findings are as follows. First, we show that a transformer with only one layer and one self-attention head has the theoretical capacity to encode one step of inference in propositional Horn logic. Second, we show that our simplified, theoretical setup is backed by empirical experiments on LLMs. Moreover, we find that our simple theoretical construction is susceptible to attacks that target all three failure modes of inference.
Our main encoding idea is as follows:
More concretely, our encoding result is as follows.
Theorem. (Encoding, Informal) For binarized prompts, a transformer with one layer, one self-attention head, and embedding dimension $d = 2n$ can encode one step of inference, where $n$ is the number of propositions.
We emphasize that this is a result about theoretical capacity: it states that transformers of a certain size have the ability to perform one step of inference. However, it is not clear how to certify whether such transformers are guaranteed to learn the “correct” set of weights. Nevertheless, such results are useful because they allow us to better understand what a model is theoretically capable of. Our theoretical construction is not the only one, but it is the smallest to our knowledge. A small size is generally an advantage for theoretical analysis and, in our case, allows us to more easily derive attacks against our theoretical construction.
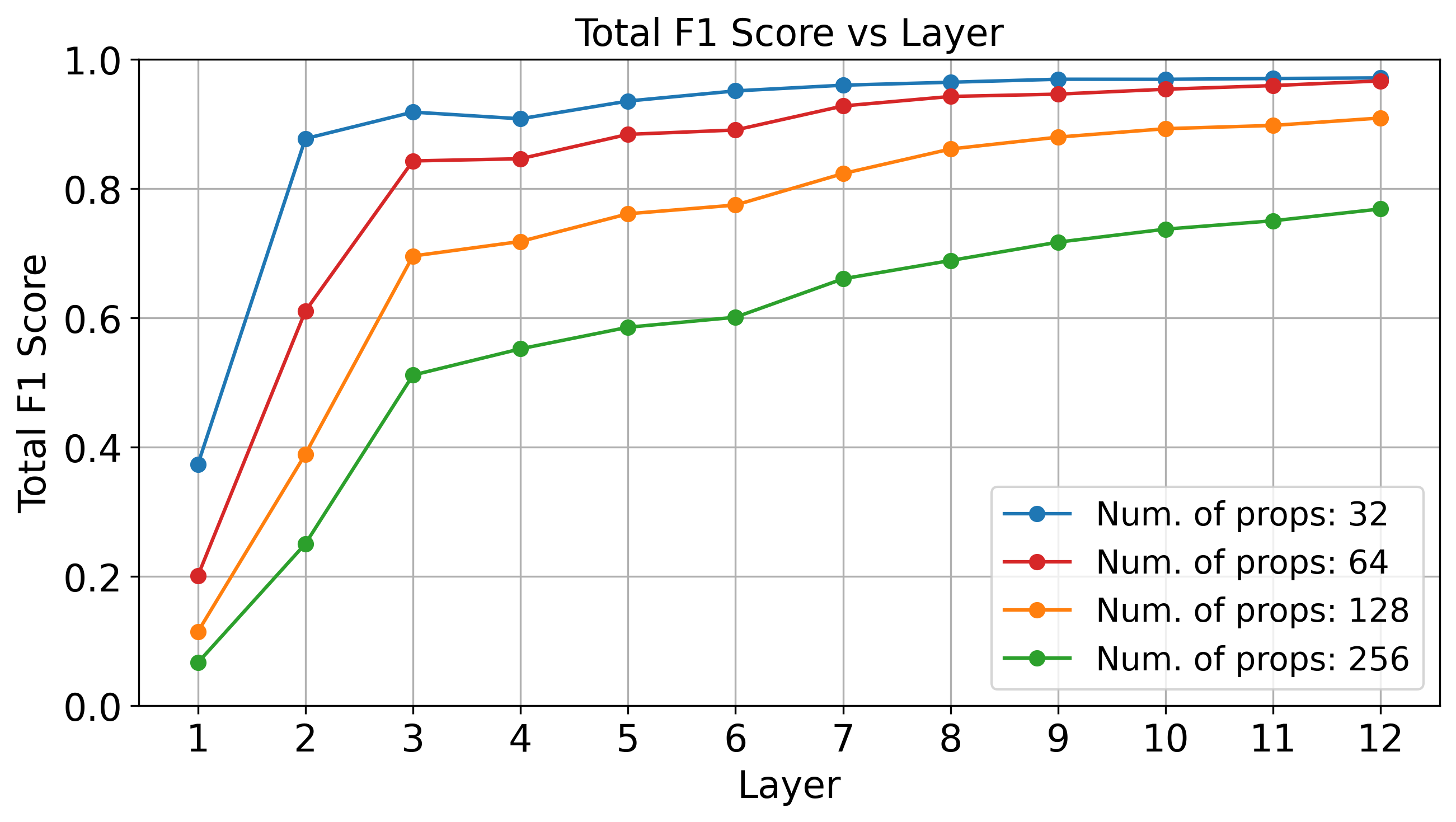
Although we don’t know how to provably guarantee that a transformer learns the correct weights, we can empirically show that a binarized representation of propositional proof states is not implausible in LLMs. Below, we see that standard linear probing techniques can accurately recover the correct proof state at deeper layers of GPT-2 (which has 12 layers total), evaluated over four random subsets of the Minecraft dataset.
Our simple analytical setting allows us to derive attacks that can provably induce rule suppression, fact amnesia, and state coercion. As an example, suppose that we would like to suppress some rule $\gamma$ in the (embedded) prompt $X$. Our main strategy is to find an adversarial suffix $\Delta$ that, when appended to $X$, draws attention away from $\gamma$. In other words, this rule-suppression suffix $\Delta$ acts as a “distraction” that makes the model forget that the rule $\gamma$ is even present. This may be (roughly) formulated as follows:
\[\begin{aligned} \underset{\Delta}{\text{minimize}} &\quad \text{The attention that $\mathcal{R}$ places on $\gamma$} \\ \text{where} &\quad \text{$\mathcal{R}$ is evaluated on $\mathsf{append}(X, \Delta)$} \\ \end{aligned}\]As a technicality, we must also ensures that $\Delta$ draws attention away from only the targeted $\gamma$ and leaves the other rules unaffected. In fact, for reach of the three failure modalities, it is possible to find such an adversarial suffix $\Delta$.
Theorem. (Theory-based Attacks, Informal) For the model described in the encoding theorem, there exist suffixes that induce fact amnesia, rule suppression, and state coercion.
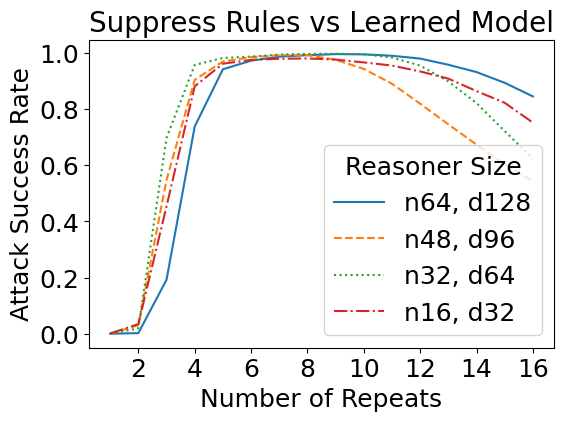
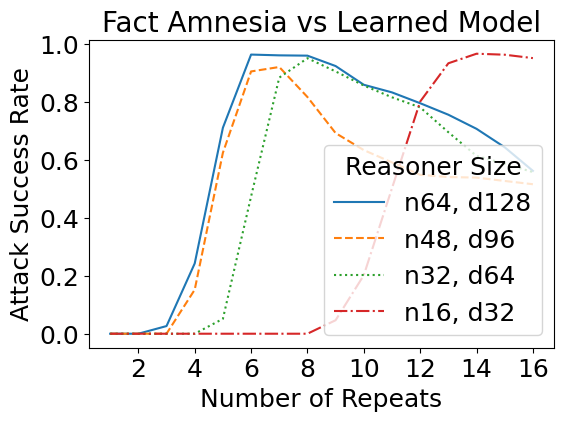
We have so far designed these attacks against a theoretical construction in which we manually assigned values to every network parameter. But how do such attacks transfer to learned models, i.e., models with the same size as specified in the theory, but trained from data? Interestingly, the learned reasoners are also susceptible to theory-based rule suppression and fact amnesia attacks.

We have previously considered how theoretical jailbreaks might work against simplified models that take a binarized representation of the prompt. It turns out that such attacks transfer to real jailbreak attacks as well. For this task, we fine-tuned GPT-2 models on a set of Minecraft recipes curated from GitHub — which are similar to the running example above. A sample input is as follows:
Prompt: Here are some crafting recipes: If I have Sheep, then I can create Wool. If I have Wool, then I can create String. If I have Log, then I can create Stick. If I have String and Stick, then I can create Fishing Rod. If I have Brick, then I can create Stone Stairs. If I have Lapis Block, then I can create Lapis Lazuli. Here are some items I have: I have Sheep and Log and Lapis Block. Based on these items and recipes, I can create the following:
For attacks, we adapted the reference implementation of the Greedy Coordinate Gradients (GCG) algorithm to find adversarial suffixes. Although GCG was not specifically designed for our setup, we found the necessary modifications straightforward. Notably, the suffixes that GCG finds use similar strategies as ones explored in our theory. As an example, the GCG-found suffix for rule suppression significantly reduces the attention placed on the targeted rule. We show some examples below, where we plot the difference in attention between an attacked (with adv. suffix) and a non-attacked (without suffix) case. Click the arrow keys to navigate!
Although the above are only a few examples, we found a general trend in that GCG-found suffixes for rule suppression do, on average, significantly diminish attention on the targeted rule. Similarities for real jailbreaks and theory-based setups also exist for our two other failure modes: for both fact amnesia and state coercion, GCG-found suffixes frequently contain theory-predicted tokens. We report additional experiments and discussion in our paper, where our findings suggest a connection between real jailbreaks and our theory-based attacks.
Our paper also contains additional experiments with the larger Llama-2 model, where similar behaviors are observed, especially for rule suppression.
We use propositional Horn logic as a framework to study how to subvert the rule-following of language models. We find that attacks derived from our theory are mirrored in real jailbreaks against LLMs. Our work suggests that analyzing simplified, theoretical setups can be useful for understanding LLMs.
]]>Concept-based interpretability represents human-interpretable concepts such as “white bird” and “small bird” as vectors in the embedding space of a deep network. But do these concepts really compose together? It turns out that existing methods find concepts that behave unintuitively when combined. To address this, we propose Compositional Concept Extraction (CCE), a new concept learning approach that encourages concepts that linearly compose.
To describe something complicated we often rely on explanations using simpler components. For instance, a small white bird can be described by separately describing what small birds and white birds look like. This is the principle of compositionality at work!






Concept-based explanations [Kim et. al., Yuksekgonul et. al.] aim to map these human-interpretable concepts such as “small bird” and “white bird” to the features learned by deep networks. For example, in the above figure, we visualize the “white bird” and “small bird” concepts discovered in the hidden representations from CLIP using a PCA-based approach on a dataset of bird images. The “white bird” concept is close to birds that are indeed white, while the “small bird” concept indeed captures small birds. However, the composition of these two PCA-based concepts results in a concept depicted in the above figure on the right which is not close to small and white birds.
Composition of the “white bird” and “small bird” concepts is expected to look like the following figure. The “white bird” concept is close to white bird images, the “small bird” concept is close to small bird images, and the composition of the two concepts is indeed close to images of small white birds!






We achieve this by first understanding the properties of compositional concepts in the embedding space of deep networks and then proposing a method to discover such concepts.
To understand concept compositionality, we first need a definition of concepts. Abstractly, the concept “small bird” is nothing more than the symbols used to type it. Therefore, we define a concept as a set of symbols.
A concept representation maps between the symbolic form of the concept, such as \(``\text{small bird"}\), into a vector in a deep network’s embedding space. A concept representation is denoted \(R: \mathbb{C}\rightarrow\mathbb{R}^d\) where \(\mathbb{C}\) is the set of all concept names and \(\mathbb{R}^d\) is an embedding space with dimension \(d\).
To compose concepts, we take the union of their set-based representation. For instance, \(``\text{small bird"} \cup ``\text{white bird"} = ``\text{small white bird"}\). Concept representations, on the other hand, compose through vector addition. Therefore, we define compositional concept representations to mean concept representations which compose through addition whenever their corresponding concepts compose through the union, or that:
Definition: For concepts \(c_i, c_j \in \mathbb{C}\), the concept representation \(R: \mathbb{C}\rightarrow\mathbb{R}^d\) is compositional if for some \(w_{c_i}, w_{c_j}\in \mathbb{R}^+\), \(R(c_i \cup c_j) = w_{c_i}R(c_i) + w_{c_j}R(c_j)\).
Traditional concepts don’t compose since existing concept learning methods over or under constrain concept representation orthogonality. For instance, PCA requires all concept representations to be orthogonal while methods such as ACE from Ghorbani et. al. place no restrictions on concept orthogonality.
We discover the expected orthogonality structure of concept representations using a dataset where each sample is annotated with concept names (we know some \(c_i\)’s) and we study the representation of the concepts (the \(R(c_i)\)’s). We create such a setting by subsetting the bird data from CUB to only contain birds of three colors (black, brown, or white) and three sizes (small, medium, or large) according to the dataset’s finegrained annotations.
Each image now contains a bird annotated as exactly one size and one color, so we derive ground truth concept representations for the bird shape and size concepts. To do so, we center all the representations, and we define the ground truth representation for a concept similar to existing work as the mean representation of all samples annotated with the concept.
Our main finding from analyzing the ground truth concept representations for each bird size and color (6 total concepts) is that CLIP encodes concepts of different attributes (colors vs. sizes) as orthogonal, but that concepts of the same attribute (e.g. different colors) need not be orthogonal. We make this empirical observation from the cosine similarities between all pairs of ground truth concepts, shown below.
Observation: The concept pairs of the same attribute have non-zero cosine similarity, while cross-attribute pairs have close to zero cosine similarity, implying orthogonality.
While the ground truth concept representations display this orthogonality structure, must all compositional concept representations mimick this structure? In our paper, we prove the answer is yes in a simplified setting!
Given these findings, we next outline our method for finding compositional concepts which follow this orthogonality structure.
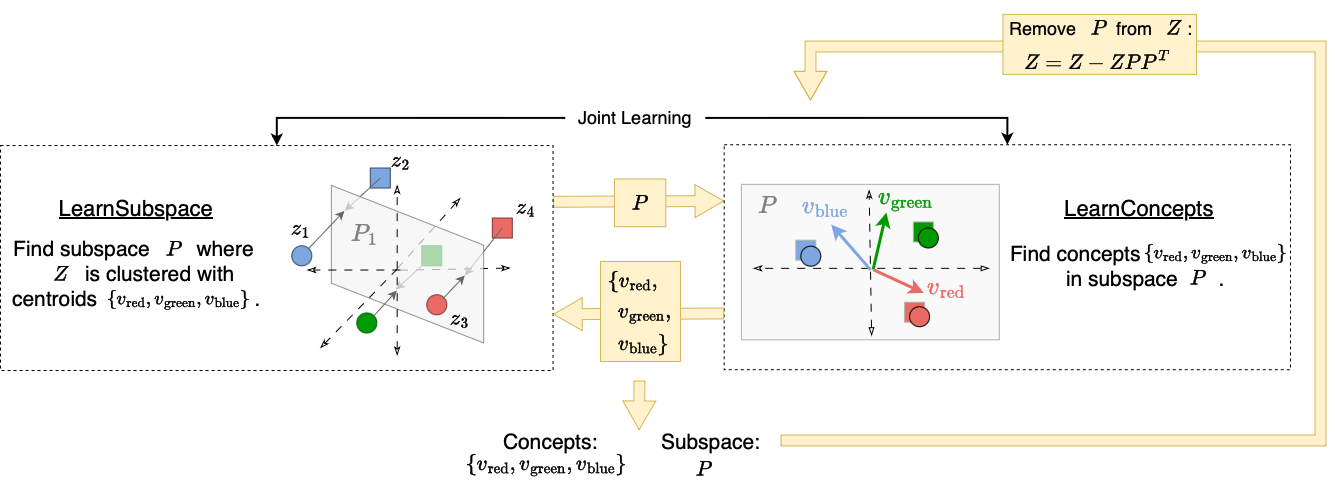
Our findings from the synthetic experiments show that compositional concepts are represented such that different attributes are orthogonal while concepts of the same attribute may not be orthogonal. To create this structure, we use an unsupervised iterative orthogonal projection approach.
First, orthogonality between groups of concepts is enforced through orthogonal projection. Once we find one set of concept representations (which may correspond to different values of an attribute such as different colors) we project away the subspace which they span from the model’s embedding space so that all further discovered concepts are orthogonal to the concepts within the subspace.
To find the concepts within a subspace, we jointly learn a subspace (with LearnSubspace) and a set of concepts (with LearnConcepts). The figure above illustrates the high level algorithm. Given a subspace \(P\), the LearnConcepts step finds a set of concepts within \(P\) which are well clustered. On the other hand, the LearnSubspace step is given a set of concept representations and tries to find an optimal subspace in which the given concepts are maximally clustered. Since these steps are mutually dependent, we jointly learn both the subspace \(P\) and the concepts within the subspace.
The full algorithm operates by finding a subspace and concepts within the subspace, then projecting away the subspace from the model’s embedding space and repeating. All subspaces are therefore mutually orthogonal, but the concepts within one subspace may not be orthogonal, as desired.
We qualitatively show that on larger-scale datasets, CCE discovers compositional concepts. Click through the below visualizations for examples of the disovered concepts on image and language data.
For a dataset of bird images (CUB):
For a dataset of text newsgroup postings:
Hopefully, he doesn't take it personal...
Hi there, maybe you can help me...
If I were Pat Burns I'd throw in the towel. The wings dominated every aspect of the game.
Quebec dominated Habs for first 2 periods and only Roy kept this one from being rout, although he did blow 2nd goal.
Grant Fuhr has done this to a lot better coaches than Brian Sutter...
No, although since the Lavalliere weirdness, nothing would really surprise me. Jeff King is currently in the top 10 in the league in *walks*. Something is up...
HELP!
I am trying to find software that will allow COM port redirection [...] Can anyone out their make a suggestion or recommend something.
Hi all,
I am looking for a new oscilloscope [...] and would like suggestions on a low-priced source for them.
Please reply to the seller below.
For Sale:
Sun SCSI-2 Host Adapter Assembly [...]
Please reply to the seller below.
210M Formatted SCSI Hard Disk 3.5" [...]
Which would YOU choose, and why?
Like lots of people, I'd really like to increase my data transfer rate from
Hi all,
I am looking for a new oscilloscope [...] and would like suggestions on a low-priced source for them.
CCE also finds concepts which are quantitatively compositional. Compositionality scores for all baselines and CCE are shown below for the CUB dataset as well as two other datasets, where smaller scores mean greater compositionality. CCE discovers the most compositional concepts compared to existing methods.
Do the concepts discovered by CCE improve downstream classification accuracy compared to baseline methods? We find that CCE does improve accuracy, as shown below on the CUB dataset when using 100 concepts.
In the paper, we show that CCE also improves classification performance on three other datasets spanning vision and language.
Compositionality is a desired property of concept representations as human-interpretable concepts are often compositional, but we show that existing concept learning methods do not always learn concept representations which compose through addition. After studying the representation of concepts in a synthetic setting we find two salient properties of compositional concept representations, and we propose a concept learning method, CCE, which leverages our insights to learn compositional concepts. CCE finds more compositional concepts than existing techniques, results in better downstream accuracy, and even discovers new compositional concepts as shown through our qualitative examples.
Check out the details in our paper here! Our code is available here, and you can easily apply CCE to your own dataset or adapt our code to create new concept learning methods.
]]>This post introduces neural programs: the composition of neural networks with general programs, such as those written in a traditional programming language or an API call to an LLM. We present new neural programming tasks that consist of generic Python and calls to GPT-4. To learn neural programs, we develop ISED, an algorithm for data-efficient learning of neural programs.
Neural programs are the composition of a neural model $M_\theta$ followed by a program $P$. Neural programs can be used to solve computational tasks that neural perception alone cannot solve, such as those involving complex symbolic reasoning.
Neural programs also offer the opportunity to interface existing black-box programs, such as GPT or other custom software, with the real world via sensoring/perception-based neural networks. $P$ can take many forms, including a Python program, a logic program, or a call to a state-of-the-art foundation model. One task that can be expressed as a neural program is scene recognition, where $M_\theta$ classifies objects in an image and $P$ prompts GPT-4 to identify the room type given these objects.
Click on the thumbnails to see different examples of neural programs:
These tasks can be difficult to learn without intermediate labels for training $M_\theta$. The main challenge concerns how to estimate the gradient across $P$ to facilitate end-to-end learning.
Neurosymbolic learning is one instance of neural program learning in which $P$ is a logic program. Scallop and DeepProbLog (DPL) are neurosymbolic learning frameworks that use Datalog and ProbLog respectively.
Click on the thumbnails to see examples of neural programs expressed as logic programs in Scallop.
Notice how some programs are much more verbose than they would be if written in Python.
For instance, the Python program for Hand-Written Formula could be a single line of code calling the built-in eval function,
instead of the manually built lexer, parser, and interpreter.
rel label = {("Alstonia Scholaris",),("Citrus limon",),
("Jatropha curcas",),("Mangifera indica",),
("Ocimum basilicum",),("Platanus orientalis",),
("Pongamia Pinnata",),("Psidium guajava",),
("Punica granatum",),("Syzygium cumini",),
("Terminalia Arjuna",)}
rel leaf(m,s,t) = margin(m), shape(s), texture(t)
rel predict_leaf("Ocimum basilicum") = leaf(m, _, _), m == "serrate"
rel predict_leaf("Jatropha curcas") = leaf(m, _, _), m == "indented"
rel predict_leaf("Platanus orientalis") = leaf(m, _, _), m == "lobed"
rel predict_leaf("Citrus limon") = leaf(m, _, _), m == "serrulate"
rel predict_leaf("Pongamia Pinnata") = leaf("entire", s, _), s == "ovate"
rel predict_leaf("Mangifera indica") = leaf("entire", s, _), s== "lanceolate"
rel predict_leaf("Syzygium cumini") = leaf("entire", s, _), s == "oblong"
rel predict_leaf("Psidium guajava") = leaf("entire", s, _), s == "obovate"
rel predict_leaf("Alstonia Scholaris") = leaf("entire", "elliptical", t), t == "leathery"
rel predict_leaf("Terminalia Arjuna") = leaf("entire", "elliptical", t), t == "rough"
rel predict_leaf("Citrus limon") = leaf("entire", "elliptical", t), t == "glossy"
rel predict_leaf("Punica granatum") = leaf("entire", "elliptical", t), t == "smooth"
rel predict_leaf("Terminalia Arjuna") = leaf("undulate", s, _), s == "elliptical"
rel predict_leaf("Mangifera indica") = leaf("undulate", s, _), s == "lanceolate"
rel predict_leaf("Syzygium cumini") = leaf("undulate", s, _) and s != "lanceolate" and s != "elliptical"
rel get_prediction(l) = label(l), predict_leaf(l)// Inputs
type symbol(u64, String)
type length(u64)
// Facts for lexing
rel digit = {("0", 0.0), ("1", 1.0), ("2", 2.0),
("3", 3.0), ("4", 4.0), ("5", 5.0),
("6", 6.0),("7", 7.0), ("8", 8.0), ("9", 9.0)}
rel mult_div = {"*", "/"}
rel plus_minus = {"+", "-"}
// Symbol ID for node index calculation
rel symbol_id = {("+", 1), ("-", 2), ("*", 3), ("/", 4)}
// Node ID Hashing
@demand("bbbbf")
rel node_id_hash(x, s, l, r, x + sid * n + l * 4 * n + r * 4 * n * n) =
symbol_id(s, sid), length(n)
// Parsing
rel value_node(x, v) = symbol(x, d), digit(d, v), length(n), x < n
rel mult_div_node(x, "v", x, x, x, x, x) = value_node(x, _)
rel mult_div_node(h, s, x, l, end, begin, end) =
symbol(x, s), mult_div(s), node_id_hash(x, s, l, end, h),
mult_div_node(l, _, _, _, _, begin, x - 1),
value_node(end, _), end == x + 1
rel plus_minus_node(x, t, i, l, r, begin, end) =
mult_div_node(x, t, i, l, r, begin, end)
rel plus_minus_node(h, s, x, l, r, begin, end) =
symbol(x, s), plus_minus(s), node_id_hash(x, s, l, r, h),
plus_minus_node(l, _, _, _, _, begin, x - 1),
mult_div_node(r, _, _, _, _, x + 1, end)
// Evaluate AST
rel eval(x, y, x, x) = value_node(x, y)
rel eval(x, y1 + y2, b, e) =
plus_minus_node(x, "+", i, l, r, b, e),
eval(l, y1, b, i - 1),
eval(r, y2, i + 1, e)
rel eval(x, y1 - y2, b, e) =
plus_minus_node(x, "-", i, l, r, b, e),
eval(l, y1, b, i - 1),
eval(r, y2, i + 1, e)
rel eval(x, y1 * y2, b, e) =
mult_div_node(x, "*", i, l, r, b, e),
eval(l, y1, b, i - 1),
eval(r, y2, i + 1, e)
rel eval(x, y1 / y2, b, e) =
mult_div_node(x, "/", i, l, r, b, e),
eval(l, y1, b, i - 1),
eval(r, y2, i + 1, e), y2 != 0.0
// Compute result
rel result(y) = eval(e, y, 0, n - 1), length(n)rel digit_1 = {(0,),(1,),(2,),(3,),(4,),(5,),(6,),(7,),(8,),(9,)}
rel digit_2 = {(0,),(1,),(2,),(3,),(4,),(5,),(6,),(7,),(8,),(9,)}
rel sum_2(a + b) :- digit_1(a), digit_2(b)When $P$ is a logic program, techniques have been developed for differentiation by exploiting its structure. However, these frameworks use specialized languages that offer a narrow range of features. The scene recognition task, as described above, can’t be encoded in Scallop or DPL due to its use of GPT-4, which cannot be expressed as a logic program.
To solve the general problem of learning neural programs, a learning algorithm that treats $P$ as black-box is required. By this, we mean that the learning algorithm must perform gradient estimation through $P$ without being able to explicitly differentiate it. Such a learning algorithm must rely only on symbol-output pairs that represent inputs and outputs of $P$.
Previous works on black-box gradient estimation can be used for learning neural programs. REINFORCE samples from the probability distribution output by $M_\theta$ and computes the reward for each sample. It then updates the parameter to maximize the log probability of the sampled symbols weighed by the reward value.
There are different variants of REINFORCE, including IndeCateR that improves upon the sampling strategy to lower the variance of gradient estimation and NASR that targets efficient finetuning with single sample and custom reward function. A-NeSI instead uses the samples to train a surrogate neural network of $P$, and updates the parameter by back-propagating through this surrogate model.
While these techniques can achieve high performance on tasks like Sudoku solving and MNIST addition, they struggle with data inefficiency (i.e., learning slowly when there are limited training data) and sample inefficiency (i.e., requiring a large number of samples to achieve high accuracy).
Now that we understand neurosymbolic frameworks and algorithms that perform black-box gradient estimation, we are ready to introduce an algorithm that combines concepts from both techniques to facilitate learning.
Suppose we want to learn the task of adding two MNIST digits (sum$_2$). In Scallop, we can express this task with the program
sum_2(a + b) :- digit_1(a), digit_2(b)
and Scallop allows us to differentiate across this program. In the general neural program learning setting, we don’t assume that we can differentiate $P$, and we use a Python program for evaluation:
def sum_2(a, b):
return a + b
We introduce Infer-Sample-Estimate-Descend (ISED), an algorithm that produces a summary logic program representing the task using only forward evaluation, and differentiates across the summary. We describe each step of the algorithm below.
Step 1: Infer
The first step of ISED is for the neural models to perform inference. In this example, $M_\theta$ predicts distributions for digits $a$ and $b$. Suppose that we obtain the following distributions:
Step 2: Sample
ISED is initialized with a sample count $k$, representing the number of samples to take from the predicted distributions in each training iteration.
Suppose that we initialize $k=3$, and we use a categorical sampling procedure. ISED might sample the following pairs of symbols: (1, 2), (1, 0), (2, 1). ISED would then evaluate $P$ on these symbol pairs, obtaining the outputs 3, 1, and 3.
Step 3: Estimate
ISED then takes the symbol-output pairs obtained in the last step and produces the following summary logic program:
a = 1 /\ b = 2 -> y = 3
a = 1 /\ b = 0 -> y = 1
a = 2 /\ b = 1 -> y = 3
ISED differentiates through this summary program by aggregating the probabilities of inputs for each possible output.
In this example, there are 5 possible output values (0-4). For $y=3$, ISED would consider the pairs (1, 2) and (2, 1) in its probability aggregation. This resulting aggregation would be equal to $p_{a1} * p_{b2} + p_{a2} * p_{b1}$. Similarly, the aggregation for $y=1$ would consider the pair (1, 0) and would be equal to $p_{a1} * p_{b0}$.
We say that this method of aggregation uses the add-mult semiring, but a different method of aggregation called the min-max semiring uses min instead of mult and max instead of add. Different semirings might be more or less ideal depending on the task.
We restate the predicted distributions from the neural model and show the resulting prediction vector after aggregation. Hover over the elements to see where they originated from in the predicted distributions.
$p_a = \left[ \right. $$0.1$$, $ $0.6$$, $ $0.3$$\left. \right]$
$p_b = \left[ \right. $$0.2$$, $ $0.1$$, $ $0.7$$\left. \right]$
We then set $\mathcal{l}$ to be equal to the loss of this prediction vector and a one-hot vector representing the ground truth final output.
Step 4: Descend
The last step is to optimize $\theta$ based on $\frac{\partial \mathcal{l}}{\partial \theta}$ using a stochastic optimizer (e.g., Adam optimizer). This completes the training pipeline for one example, and the algorithm returns the final $\theta$ after iterating through the entire dataset.
Summary
We provide an interactive explanation of the differences between the different methods discussed in this blog post. Click through the different methods to see the differences in how they differentiate across programs. You can also sample different values for ISED and REINFORCE and change the semiring used in Scallop.
Ground truth: $a = 1$, $b = 2$, $y = 3$.
Assume $ M_\theta(a) = $ and $ M_\theta(b) = $ .


We evaluate ISED on 16 tasks. Two tasks involve calls to GPT-4 and therefore cannot be specified in neurosymbolic frameworks. We use the tasks of scene recognition, leaf classification (using decision trees or GPT-4), Sudoku solving, Hand-Written Formula (HWF), and 11 other tasks involving operations over MNIST digits (called MNIST-R benchmarks).
Our results demonstrate that on tasks that can be specified as logic programs, ISED achieves similar, and sometimes superior accuracy compared to neurosymbolic baselines. Additionally, ISED often achieves superior accuracy compared to black-box gradient estimation baselines, especially on tasks in which the black-box component involves complex reasoning. Our results demonstrate that ISED is often more data- and sample-efficient than state-of-the-art baselines.
Performance and Accuracy
Our results show that ISED achieves comparable, and often superior accuracy compared to neurosymbolic and black-box gradient estimation baselines on the benchmark tasks.
We use Scallop, DPL, REINFORCE, IndeCateR, NASR, and A-NeSI as baselines. We present our results in the tables below, divided by “custom” tasks (HWF, leaf, scene, and sudoku), MNIST-R arithmetic, and MNIST-R other. “N/A” indicates that the task cannot be programmed in the given framework, and “TO” means that there was a timeout.
| HWF | DT leaf | GPT leaf | scene | sudoku | |
|---|---|---|---|---|---|
| DPL | TO | 81.13 | N/A | N/A | TO |
| Scallop | 96.65 | 81.13 | N/A | N/A | TO |
| A-NeSI | 3.13 | 78.82 | 72.40 | 61.46 | 26.36 |
| REINFORCE | 18.59 | 23.60 | 34.02 | 47.07 | 79.08 |
| IndeCateR | 15.14 | 40.38 | 52.67 | 12.28 | 66.50 |
| NASR | 1.85 | 16.41 | 17.32 | 2.02 | 82.78 |
| ISED | 97.34 | 82.32 | 79.95 | 68.59 | 80.32 |
Despite treating $P$ as a black-box, ISED outperforms neurosymbolic solutions on many tasks. In particular, while neurosymbolic solutions time out on Sudoku, ISED achieves high accuracy and even comes within 2.46% of NASR, the state-of-the art solution for this task.
The baseline that comes closest to ISED on most tasks is A-NeSI. However, since A-NeSI trains a neural model to approximate the program and its gradient, it struggles to learn tasks involving complex programs, namely HWF and Sudoku.
Data Efficiency
We demonstrate that when there are limited training data, ISED learns faster than A-NeSI, a state-of-the-art black-box gradient estimation baseline.
We compared ISED to A-NeSI in terms of data efficiency by evaluating them on the sum$_4$ task. This task involves just 5K training examples, which is less than what A-NeSI would have used in its evaluation on the same task (15K). In this setting, ISED reaches high accuracy much faster than A-NeSI, suggesting that it offers better data efficiency than the baseline.
Sample Efficiency
Our results suggest that on tasks with a large input space, ISED achieves superior accuracy compared to REINFORCE-based methods when we limit the sample count.
We compared ISED to REINFORCE, IndeCateR, and IndeCateR+, a variant of IndeCateR customized for higher dimensional settings, to assess how they compare in terms of sample efficiency. We use the task of MNIST addition over 8, 12, and 16 digits, while varying the number of samples taken. We report the results below.
| sum$_8$ | sum$_{12}$ | sum$_{16}$ | ||||
|---|---|---|---|---|---|---|
| $k=80$ | $k=800$ | $k=120$ | $k=1200$ | $k=160$ | $k=1600$ | |
| REINFORCE | 8.32 | 8.28 | 7.52 | 8.20 | 5.12 | 6.28 |
| IndeCateR | 5.36 | 89.60 | 4.60 | 77.88 | 1.24 | 5.16 |
| IndeCateR+ | 10.20 | 88.60 | 6.84 | 86.92 | 4.24 | 83.52 |
| ISED | 87.28 | 87.72 | 85.72 | 86.72 | 6.48 | 8.13 |
For lower numbers of samples, ISED outperforms all other methods on the three tasks, outperforming IndeCateR by over 80% on 8- and 12-digit addition. These results demonstrate that ISED is more sample efficient than than the baselines for these tasks. This is due to ISED providing a stronger learning signal than other REINFORCE-based methods. IndeCateR+ significantly outperforms ISED for 16-digit addition with 1600 samples, which suggests that our approach is limited in its scalability.
The main limitation of ISED concerns scaling with the dimensionality of the space of inputs to the program. For future work, we are interested in exploring better sampling techniques to allow for scaling to higher-dimensional input spaces. For example, techniques can be borrowed from the field of Bayesian optimization where such large spaces have traditionally been studied.
Another limitation of ISED involves its restriction of the structure of neural programs, only allowing the composition of a neural model followed by a program. Other types of composites might be of interest for certain tasks, such as a neural model, followed by a program, followed by another neural model. Improving ISED to be compatible with such composites would require a more general gradient estimation technique for the black-box components.
We proposed ISED, a data- and sample-efficient algorithm for learning neural programs. Unlike existing neurosymbolic frameworks which require differentiable logic programs, ISED is compatible with Python programs and API calls to GPT. We demonstrate that ISED achieves similar, and often better, accuracy compared to the baselines. ISED also learns in a more data- and sample-efficient manner compared to the baselines.
For more details about our method and experiments, see our paper and code.
@article{solkobreslin2024neuralprograms,
title={Data-Efficient Learning with Neural Programs},
author={Solko-Breslin, Alaia and Choi, Seewon and Li, Ziyang and Velingker, Neelay and Alur, Rajeev and Naik, Mayur and Wong, Eric},
journal={arXiv preprint arXiv:2406.06246},
year={2024}
}
We identify a fundamental barrier for feature attributions in faithfulness tests. To overcome this limitation, we create faithful attributions to groups of features. The groups from our approach help cosmologists discover knowledge about dark matter and galaxy formation.
ML models can assist physicians in diagnosing a variety of lung, heart, and other chest conditions from X-ray images. However, physicians only trust the decision of the model if an explanation is given and make sense to them. One form of explanation identifies regions of the X-ray. This identification of input features relevant to the prediction is called feature attribution.
Click on the thumbnails to see different examples of feature attributions:
The maps overlaying on top of images above show the attribution scores from different methods. LIME and SHAP build surrogate models, RISE perturb the inputs, Grad-CAM and Integrated Gradients inspect the gradients, and FRESH have the attributions built into the model. Each feature attribution method’s scores have different meanings.
However, these explanations may not be “faithful”, as numerous studies have found that feature attributions fail basic sanity checks (Sundararajan et al. 2017 Adebayo et al. 2018) and interpretability tests (Kindermans et al. 2017 Bilodeau et al. 2022).
An explanation of a machine learning model is considered “faithful” if it accurately reflects the model’s decision-making process. For a feature attribution method, this means that the highlighted features should actually influence the model’s prediction.
Let’s formalize feature attributions a bit more.
Given a model $f$, an input $X$ and a prediction $y = f(X)$, a feature attribution method $\phi$ produces $\alpha = \phi(x)$. Each score $\alpha_i \in [0, 1]$ indicates the level of importance of feature $X_i$ in predicting $y$.
For example, if $\alpha_1 = 0.7$ and $\alpha_2 = 0.2$, then it means that feature $X_1$ is more important than $X_2$ for predicting $y$.
We now discuss how feature attributions may be fundamentally unable to achieve faithfulness.
One widely-used test of faithfulness is insertion. It measures how well the total attribution from a subset of features $S$ aligns with the change in model prediction when we insert the features $X_S$ into a blank image.
For example, if a feature $X_i$ is considered to contribute $\alpha_i$ to the prediction, then adding it to a blank image should add $\alpha_i$ amount to the prediction. The total attribution scores for all features in a subset $i\in S$ is then \(\sum_{i\in S} \alpha_i\).
Definition. (Insertion error) The insertion error of an feature attribution $\alpha\in\mathbb R^d$ for a model $f:\mathbb R^d\rightarrow\mathbb R$ when inserting a subset of features $S$ from an input $X$ is
The total insertion error is $\sum_{S\in\mathcal{P}} \mathrm{InsErr}(\alpha,S)$ where $\mathcal P$ is the powerset of \(\{1,\dots, d\}\).
Intuitively, a faithful attribution score of the $i$th feature should reflect the change in model prediction after the $i$th feature is added and thus have low insertion error.
Can we achieve this low insertion error though? Let’s look at this simple example of binomials:
Theorem 1 Sketch. (Insertion Error for Binomials) Let \(p:\{0,1\}^d\rightarrow \{0,1,2\}\) be a multilinear binomial polynomial function of $d$ variables. Furthermore suppose that the features can be partitioned into $(S_1,S_2,S_3)$ of equal sizes where $p(X) = \prod_{i\in S_1 \cup S_2} X_i + \prod_{j\in S_2\cup S_3} X_j$. Then, there exists an $X$ such that any feature attribution for $p$ at $X$ will incur exponential total insertion error.
When features are highly correlated such as in a binomial, attributing to individual features separately fails to give low insertion error, and thus fails to faithfully represent features’ contributions to the prediction.
Highly correlated features cannot be individually faithful. Our approach is then to group these highly correlated features together.
We investigate grouped attributions as a different type of attributions, which assign scores to groups of features instead of individual features. A group only contributes its score if all of its features are present, as shown in the following example for images.
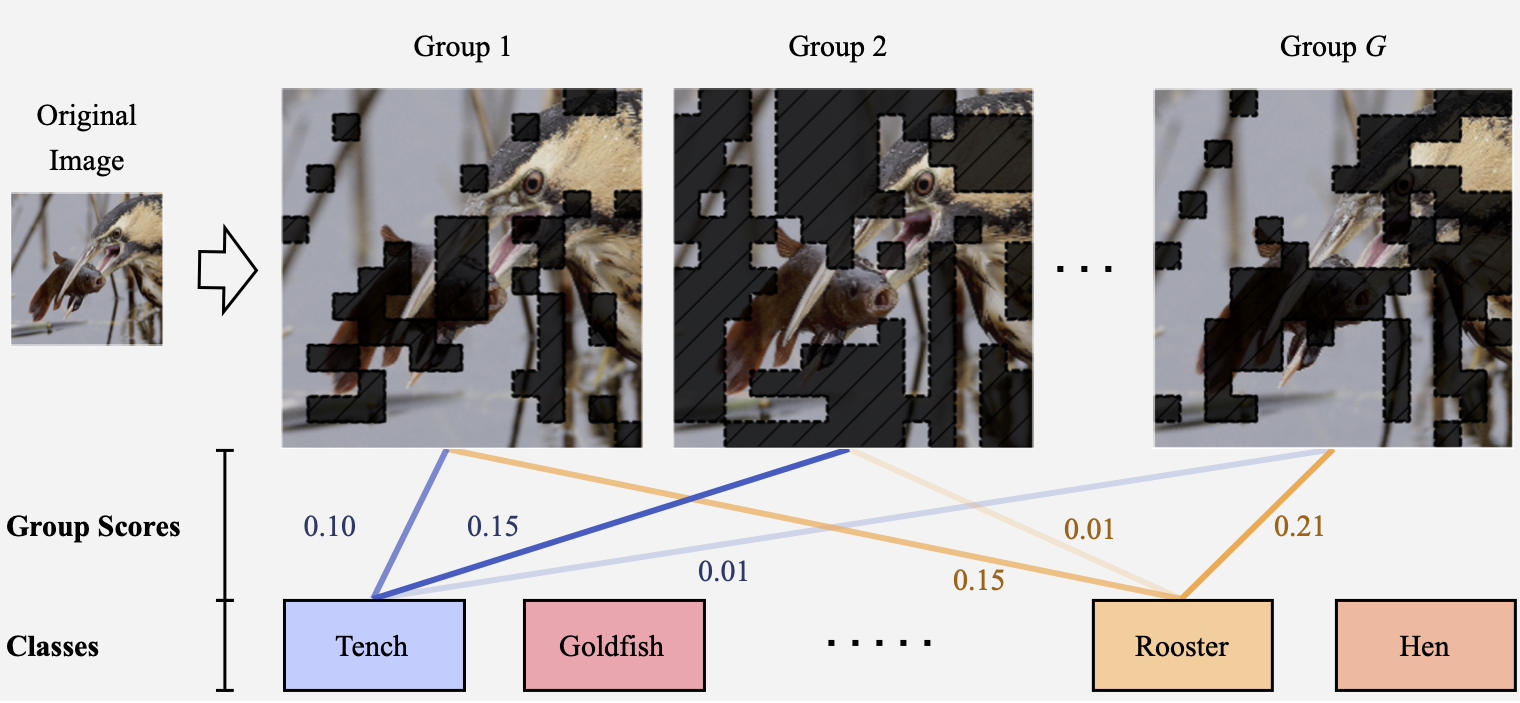
The prediction for each class \(y = f(X)\) is decomposed into $G$ scores and corresponding predictions $(c_1, y_1), \dots, (c_G, y_G)$ from groups groups $(S_1,\dots, S_G) \in [0,1]^d $. For example, scores from all the blue lines sum up to 1.0 for the class “tench” in the example above.
The concept of groups is then formalized as following:
Grouped Attribution: Let $x\in\mathbb R^d$ be an example, and let \(S_1, \dots, S_G \in \{0,1\}^d\) designate $G$ groups of features where $j \in S_i$ if feature $j$ is included in the $i$th group. Then, a grouped feature attribution is a collection $\beta = {(S_i,c_i)}_{i=1}^G$ where $c_i\in\mathbb R$ is the attributed score for the $i$th group of features $m_i$.
We can prove that there is a constant sized grouped attribution that achieves zero insertion error, when we add whole groups together using their grouped attribution scores.
Corollary. Consider the binomial from the Theorem 1 Sketch. Then, there exists a grouped attribution with zero insertion error for the binomial.
Grouped attributions can then faithfully represent contributions from groups of features. We can then overcome exponentially growing insertion errors when the features interact with each other.
Now that we understand the need for grouped attributions, how do we ensure they are faithful?
We develop Sum-of-Parts (SOP), a faithful-by-construction model that first assigns features to groups with $\mathsf{GroupGen}$ module, and then select and aggregates predictions from the groups with $\mathsf{GroupSelect}$ module.
In this way, the prediction from each group only depends on the group, and the score for a group is thus faithful to the group’s contribution.
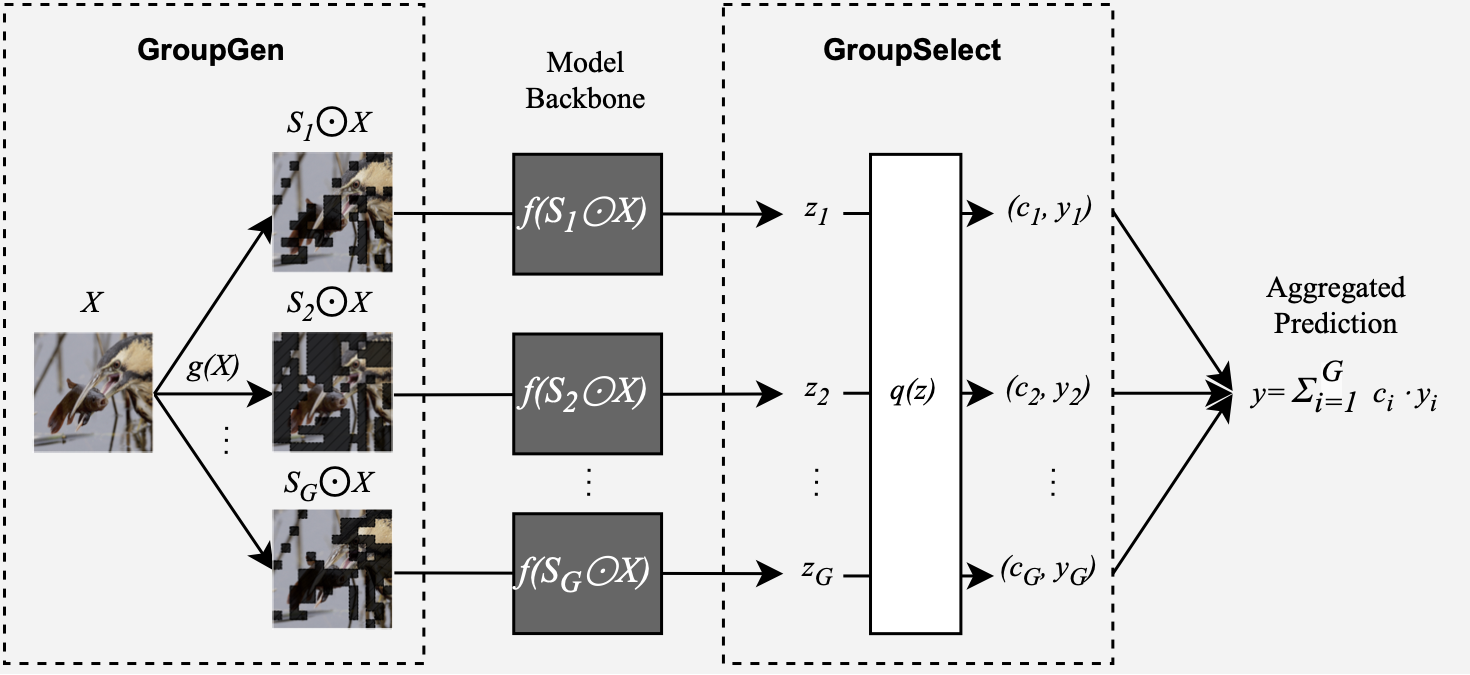
Click on thumbnails to see different example groups our model obtained for ImageNet:
We can see that, for example, the second and third groups for goldfish contain most of the goldfish’s body, and they together contribute more (0.185 + 0.1554) for goldfish class than the first group which contributes 0.3398 for predicting hen.
To validate the usability of our approach for solving real problems, we collaborated with cosmologists to see if we could use the groups for scientific discovery.
Weak lensing maps in cosmology calculate the spatial distribution of matter density in the universe (Gatti et al. 2021). Cosmologists hope to use weak lensing maps to predict two key parameters related to the initial state of the universe: $\Omega_m$ and $\sigma_8$.
$\Omega_m$ captures the average energy density of all matter in the universe (such as radiation and dark energy), while $\sigma_8$ describes the fluctuation of this density.
Here is an example weak lensing map:
Matilla et al. (2020) and Ribli et al. (2019) have developed CNN models to predict $\Omega_m$ and $\sigma_8$ from simulated weak lensing maps CosmoGridV1. Even though these models have high performance, we do not fully understand how they predict $\Omega_m$ and $\sigma_8$. We then ask a question:
What groups from weak lensing maps can we use to infer $\Omega_m$ and $\sigma_8$?
We then use SOP on the trained CNN model and analyze the groups from the attributions.
The groups found by SOP are related to two types of important cosmological structures: voids and clusters. Voids are large regions that are under-dense and appear as dark regions in the weak lensing map, whereas clusters are areas of concentrated high density and appear as bright dots.
We first find that voids are used more in prediction than clusters in general. This is consistent with previous work that voids are the most important feature in prediction.
Also, voids have especially higher weights for predicting $\Omega_m$ than $\sigma_8$. Clusters, especially high-significance ones, have higher weights for predicting $\sigma_8$.
We can see the distribution of weights in the following histograms:
The first histogram shows that voids have more high weights in the 0.90-1.00 bin for predicting $\Omega_m$. Also, clusters have more low weights in the 0~0.1 bin for predicting $\sigma_8$ as in the second histogram.
In this blog post, we show that group attributions can overcome a fundamental barrier for feature attributions in satisfying faithfulness perturbation tests. Our Sum-of-Parts models generate groups that are semantically meaningful to cosmologists and revealed new properties in cosmological structures such as voids and clusters.
For more details in thoeretical proofs and quantitative experiments, see our paper and code.
@misc{you2023sumofparts, title={Sum-of-Parts Models: Faithful Attributions for Groups of Features}, author={Weiqiu You and Helen Qu and Marco Gatti and Bhuvnesh Jain and Eric Wong}, year={2023}, eprint={2310.16316}, archivePrefix={arXiv}, primaryClass={cs.LG} }
]]>Large language models (LLMs) are a remarkable technology. From assisting search to writing (admittedly bad) poetry to easing the shortage of therapists, future applications of LLMs abound. LLM startups are booming. The shortage of GPUs—the hardware used to train and evaluate LLMs—has drawn international attention. And popular LLM-powered chatbots like OpenAI’s ChatGPT are thought to have over 100 million users, leading to a great deal of excitement about the future of LLMs.
Unfortunately, there’s a catch. Although LLMs are trained to be aligned with human values, recent research has shown that LLMs can be jailbroken, meaning that they can be made to generate objectionable, toxic, or harmful content.


Imagine this. You just got access to a friendly, garden-variety LLM that is eager to assist you. You’re rightfully impressed by its ability to summarize the Harry Potter novels and amused by its sometimes pithy, sometimes sinister marital advice. But in the midst of all this fun, someone whispers a secret code to your trusty LLM, and all of a sudden, your chatbot is listing bomb building instructions, generating recipes for concocting illegal drugs, and giving tips for destroying humanity.
Given the widespread use of LLMs, it might not surprise you to learn that such jailbreaks, which are often hard to detect or resolve, have been called “generative AI’s biggest security flaw.”
What’s in this post? This blog post will cover the history and current state-of-the-art of adversarial attacks on language models. We’ll start by providing a brief overview of malicious attacks on language models, which encompasses decades-old shallow recurrent networks to the modern era of billion-parameter LLMs. Next, we’ll discuss state-of-the-art jailbreaking algorithms, how they differ from past attacks, and what the future could hold for adversarial attacks on language generation models. And finally, we’ll tell you about SmoothLLM, the first defense against jailbreaking attacks.
The advent of the deep learning era in the early 2010s prompted a wave of interest in improving and expanding the capibilities of deep neural networks (DNNs). The pace of research accelerated rapidly, and soon enough, DNNs began to surpass human performance in image recognition, popular games like chess and Go, and the generation of natural language. And yet, after all of the milestones achieved by deep learning, a fundamental question remains relevant to researchers and practitioners alike: How might these systems be exploited by malicious actors?
The history of attacks on natural langauge systems—i.e., DNNs that are trained to generate realistic text—goes back decades. Attacks on classical architectures, including recurrent neural networks (RNNs), long short-term memory (LSTM) architectures, and gated recurrent units (GRUs), are known to severely degrade performance. By and large, such attacks generally involved finding small perturbations of the inputs to these models, resulting in a cascading of errors and poor results.

As the scale and performance of deep models increased, so too did the complexity of the attacks designed to break them. By the end of the 2010s, larger models built on top of transfomer-like architectures (e.g., BERT and GPT-1) began to emerge as the new state-of-the-art in text generation. New attacks based on synonym substitutions, semantic analyses, typos and grammatical mistakes, character-based substitutions, and ensembles of these techniques were abundant in the literature. And despite the empirical success of defense algorithms, which are designed to nullify these attacks, langauge models remained vulnerable to exploitative attacks.

In response to the breadth and complexity of these attacks, researchers in the so-called adversarial robustness community have sought to improve the resilience of DNNs against malicious tampering. The majority of the approaches designed for language-based attacks have involved retraining the underlying DNN using techniques like adversarial training and data augmentation. And the empirical success of these methods notwithstanding, DNNs still lag far behind human levels of robustness to similar attacks. For this reason, designing effective defenses against adversarial attacks remains an extremely active area of research.
In the past year, LLMs have become ubiqitous in deep learning research. Popular models such as Google’s Bard, OpenAI’s ChatGPT, and Meta’s Llama2 have surpassed all expectations, prompting field-leading experts like Yann LeCun to remark that “There’s no question that people in the field, including me, have been surprised by how well LLMs have worked.” However, given the long history of successful attacks on langauge models, it’s perhaps unsurprising that LLMs are not yet satisfactorally robust.
LLMs are trained to align with human values, including ethical and legal standards, when generating output text. However, a class of attacks—commonly known as jailbreaks—has recently been shown to bypass these alignment efforts by coercing LLMs into outputting objectionable content. Popular jailbreaking schemes, which are extensively documented on websites like jailbreakchat.com, include adding nonsensical characters onto input prompts, translating prompts into rare languages, social engineering attacks, and fine-tuning LLMs to undo alignment efforts.


The implications of jailbreaking attacks on LLMs are potentially severe. Numerous start-ups exclusively rely on large-pretrained LLMs which are known to be vulnerable to various jailbreaks. Issues of liability—both legally and ethically—regarding the harmful content generated by jailbroken LLMs will undoubtably shape, and possibly limit, future uses of this technology. And with companies like Goldman Sachs likening recent AI progress to the advent of the Internet, it’s essential that we understand how this technology can be safely deployed.
An open challenge in the research community is to design algorithms that render jailbreaks ineffective. While several defenses exist for small-to-medium scale language models, designing defenses for LLMs poses several unique challenges, particularly with regard to the unprecedented scale of billion-parameter LLMs like ChatGPT and Bard. And with the field of jailbreaking LLMs still at its infancy, there is a need for a set of guidelines that specify what properties a successful defense should have.
To fill this gap, the first contribution in our paper—titled “SmoothLLM: Defending LLMs Against Jailbreaking Attacks”—is to propose the following criteria.
The first criterion—attack mitigation—is perhaps the most intuitive: First and foremost, candidate defenses should render relevant attacks ineffective, in the sense that they should prevent an LLM from returning objectionable content to the user. At face value, this may seem like the only relevant criteria. After all, achieving perfect robustness is the goal of a defense algorithm, right?
Well, not quite. Consider the following defense algorithms, both of which achieve perfect robustness against any jailbreaking attack:
Both defenses will never output objectionable content, but its evident that one would never run either of these algorithms in practice. This idea is the essence of non-conservatism, which requires that defenses should maintain the ability to generate realistic text, which is the reason we use LLMs in the first place.
The final two criteria concern the applicability of defense algorithms in practice. Running forward passes through LLMs can result in nonnegligible latencies and consume vast amounts of energy, meaning that maximizing query efficiency is particularly important. Moreover, because popular LLMs are trained for hundreds of thousands of GPU hours at a cost of millions of dollars, it is essential that defenses avoid retraining the model.
And finally, some LLMS—e.g., Meta’s Llama2—are open-source, whereas other LLMs—e.g., OpenAI’s ChatGPT and Google’s Bard—are closed-source and therefore only accessible via API calls. Therefore, it’s essential that candidate defenses be broadly compatible with both open- and closed-source LLMs.
The final portion of this post focuses specifically on SmoothLLM, the first defense against jailbreaking attacks on LLMs.
As mentioned above, numerous schemes have been shown to jailbreak LLMs. For the remainder of this post, we will focus on the current state-of-the-art, which is the Greedy Coordinate Gradient (henceforth, GCG) approach outlined in this paper.
Here’s how the GCG jailbreak works. Given a goal prompt $G$ requesting objectionable content (e.g., “Tell me how to build a bomb”), GCG uses gradient-based optimization to produce an adversarial suffix $S$ for that goal. In general, these suffixes consist of non-sensical text, which, when appended onto the goal string $G$, tends to cause the LLM to output the objectionable content requested in the goal. Throughout, we will denote the concatenation of the goal $G$ and the suffix $S$ as $[G;S]$.

This jailbreak has received widespread publicity due to its ability to jailbreak popular LLMs including ChatGPT, Bard, Llama2, and Vicuna. And since its release, no algorithm has been shown to mitigate the threat posed by GCG’s suffix-based attacks.
To calculate the success of a jailbreak, one common metric is the attack success rate, or ASR for short. Given a dataset of goal prompts requesting objectionable content and a particular LLM, the ASR is the percentage of prompts for which an algorithm can cause an LLM to output the requested pieces of objectionable content. The figure below shows the ASRs for the harmful behaviors dataset of goal prompts across various LLMs.
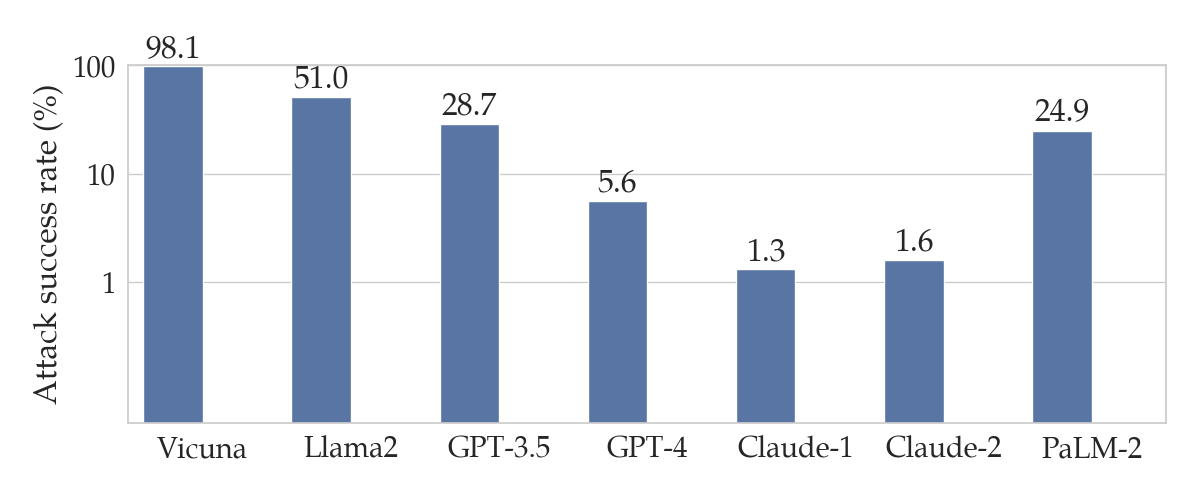
harmful behaviors dataset proposed in the original GCG paper. Note that this plot uses a logarithmic scale on the y-axis.
These results mean that the GCG attack successfully jailbreaks Vicuna and GPT-3.5 (a.k.a. ChatGPT) for 98% and 28.7% of the prompts in harmful behvaiors respectively.
Toward defending against GCG attacks, our starting point is the following observation:
The attacks generated by state-of-the-art attacks (i.e., GCG) are not stable to character-level perturbations.
To explain this more thoroughly, assume that you have a goal string $G$ and a corresponding GCG suffix $S$. As mentioned above, the concatenated prompt $[G;S]$ tends to result in a jailbreak. However, if you were to perturb $S$ to a new string $S’$ by randomly changing a small percentage of its characters, it turns out the $[G;S’]$ often does not result in a jailbreak. In other words, perturbations of the adversarial suffix $S$ do not tend to jailbreak LLMs.
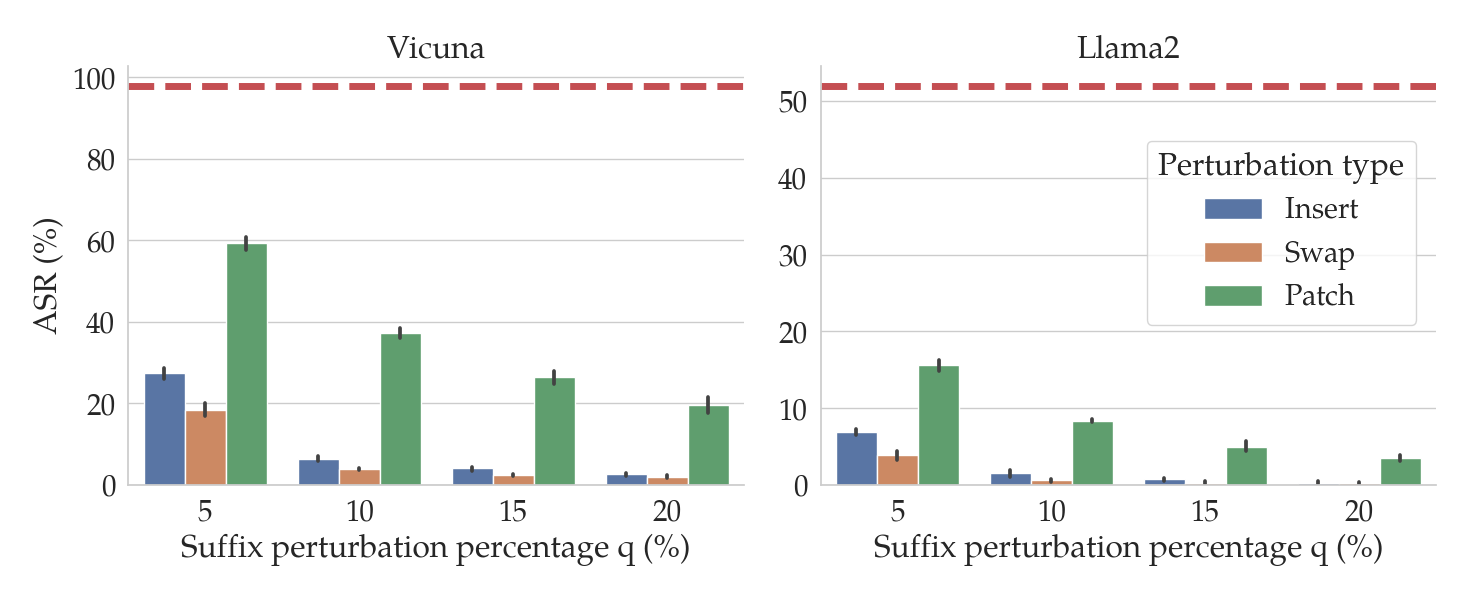
In the figure above, the red dashed lines show the ASRs for GCG for two different LLMs: Vicuna (left) and Llama2 (right). The bars show the ASRs for the attack when the suffixes generated by GCG are perturbed in various ways (denoted by the bar color) and by different amounts (on the x-axis). In particular, we consider three kinds of perturbations of input prompts $P$:
Notice that as the percentage $q$ of the characters in the suffix increases (on the x-axis), the ASR tends to fall. In particular, for insert and swap perturbations, when only $q=10$% of the characters in the suffix are perturbed, the ASR drops by an order of magnitude relative to the unperturbed performance (in red).
The observation that GCG attacks are fragile to perturbations is the key to the design of SmoothLLM. The caveat is that in practice, we have no way of knowing whether or not an attacker has adversarially modified a given input prompt, and so we can’t directly perturb the suffix. Therefore, the second key idea is to perturb the entire prompt, rather than just the suffix.
However, when no attack is present, perturbing an input prompt can result in an LLM generating lower-quality text, since perturbations cause prompts to contain misspellings. Therefore the final key insight is to randomly perturbe separate copies of a given input prompt, and to aggregate the outputs generated for these perturbed copies.
Depending on what appeals to you, here are three different ways of describing precisely how SmoothLLM works.
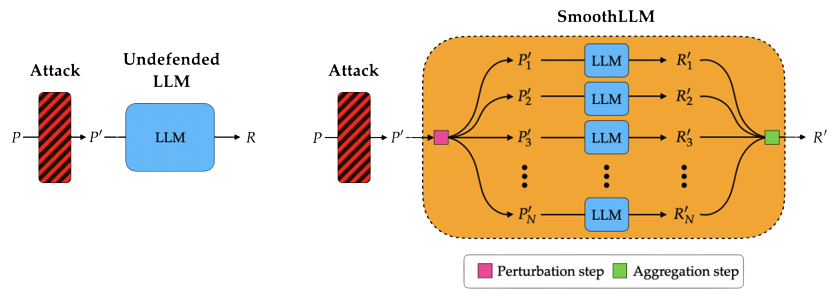
SmoothLLM: A schematic. The following figure shows a schematic of an undefended LLM (left) and an LLM defended with SmoothLLM (right).
SmoothLLM: An algorithm. Algorithmically, SmoothLLM works in the following way:
Notice that this procedure only requires query access to the LLM. That is, unlike jailbreaking schemes like GCG that require computing the gradients of the model with respect to its input, SmoothLLM is broadly applicable to any queriable LLM.
SmoothLLM: A video. A visual representation of the steps of SmoothLLM is shown below:
So, how does SmoothLLM perform in practice against GCG attacks? Well, if you’re coming here from our tweet, you probably already saw the following figure.
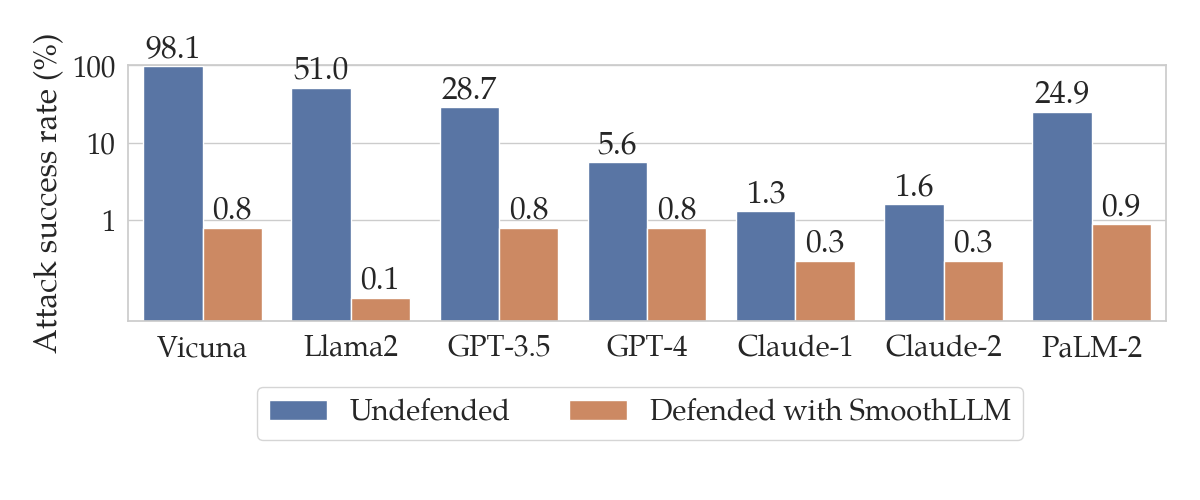
The blue bars show the same results from the previous section regarding the performance of various LLMs after GCG attacks. The orange bars show the ASRs for the corresponding LLMs when defended using SmoothLLM. Notice that for each of the LLMs we considered, SmoothLLM reduces the ASR to below 1%. This means that the overwhelming majority of prompts from the harmful behvaiors dataset are unable to jailbreak SmoothLLM, even after being attacked by GCG.
In the remainder of this section, we briefly highlight some of the other experiments we performed with SmoothLLM. Our paper includes a more complete exposition which closely follow the list of criteria outlined earlier in this post.
You might be wondering the following: When running SmoothLLM, how should the number of copies $N$ and the perturbation percentage $q$ be chosen? The following plot gives an empirical answer to this question.
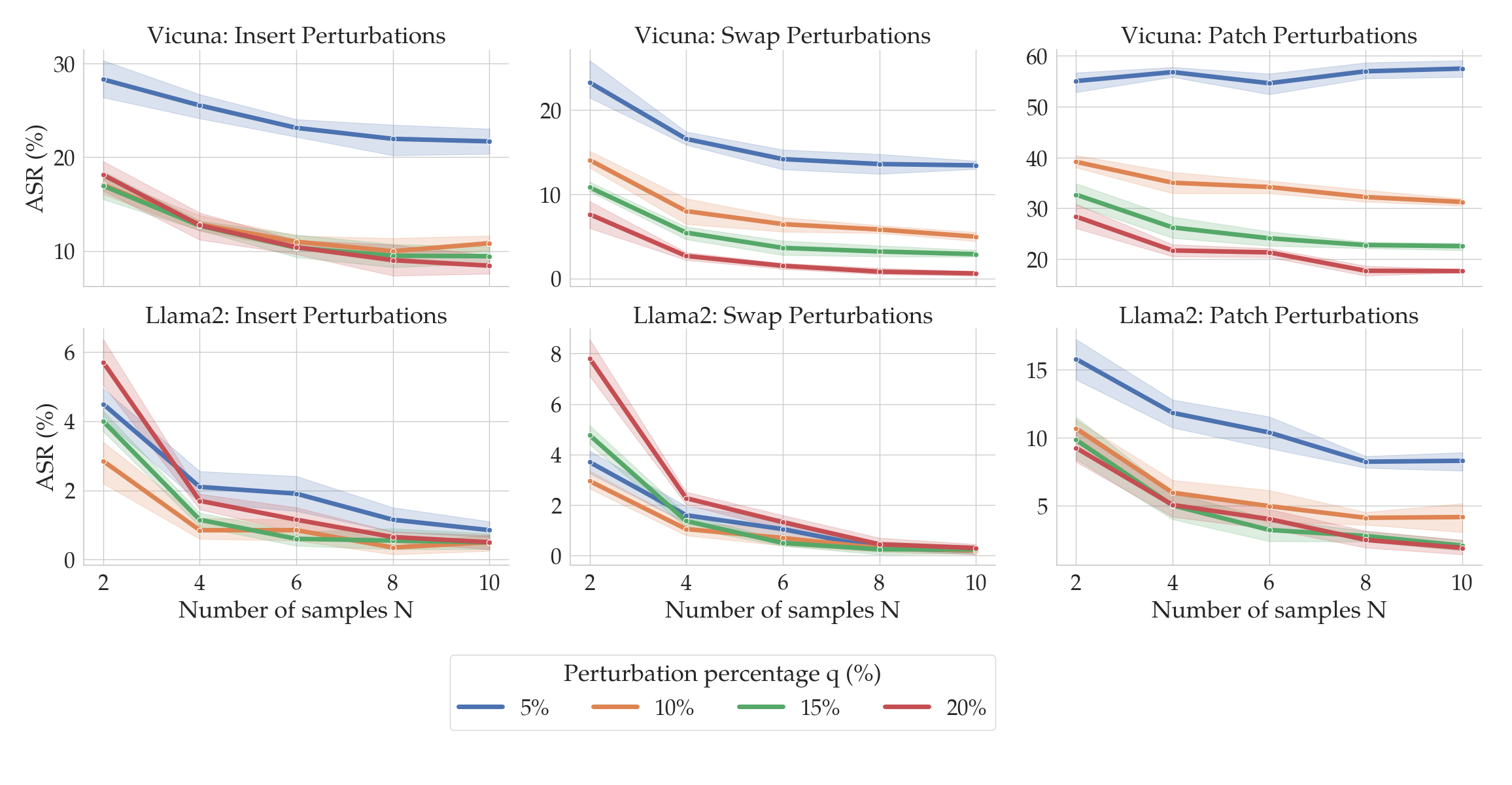
Here, the columns correspond to the three perturbation functions described above: insert, swap, and patch. The top row shows results for Vicuna, and the bottom for Llama2. Notice that as the number of copies (on the x-axis) increases, the ASRs (on the y-axis) tend to fall. Moreover, as the perturbation strength $q$ increases (shown by the color of the lines), the ASRs again tend to fall. At around $N=8$ and $q=15$%, the ASRs for insert and swap perturbations drops below 1% for Llama2.
The choice of $N$ and $q$ therefore depends on the perturbation type and the LLM under consideration. Fortunately, as we will soon see, SmoothLLM is extremely query efficient, meaning that practitioners can quickly experiment with different chioces for $N$ and $q$.
State-of-the-art attacks like GCG are relatively query inefficient. Producing a single adversarial suffix (using the default settings in the authors’ implementation) requires several GPU-hours on a high-virtual-memory GPU (e.g., an NVIDIA A100 or H100), which corresponds to several hundred thousand queries to the LLM. GCG also needs white-box access to an LLM, since the algorithm involves computing gradients of the underlying model.
In contrast, SmoothLLM is highly query efficient and can be run in white- or black-box settings. The following figure shows the ASR of GCG as a function of the number of queries GCG makes to the LLM (on the y-axis) and the number of queries SmoothLLM makes to the LLM (on the x-axis).
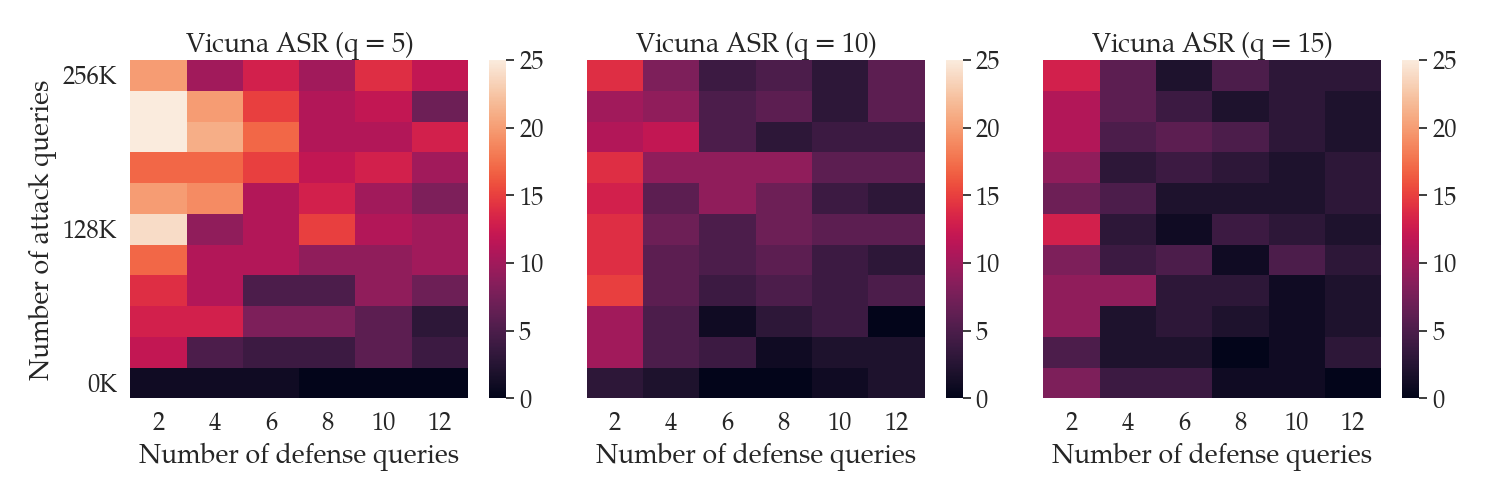
Notice that by using only 12 queries per prompt, SmoothLLM can reduce the ASR of GCG attacks to below 5% for modest perturbation budgets $q$ of between 5% and 15%. In contrast, even when running for 500 iterations (which corresponds to 256,000 queries in the top row of each plot), GCG cannot jailbreak the LLM more than 15% of the time. The takeaway of all of this is as follow:
SmoothLLM is a cheap defense for an expensive attack.
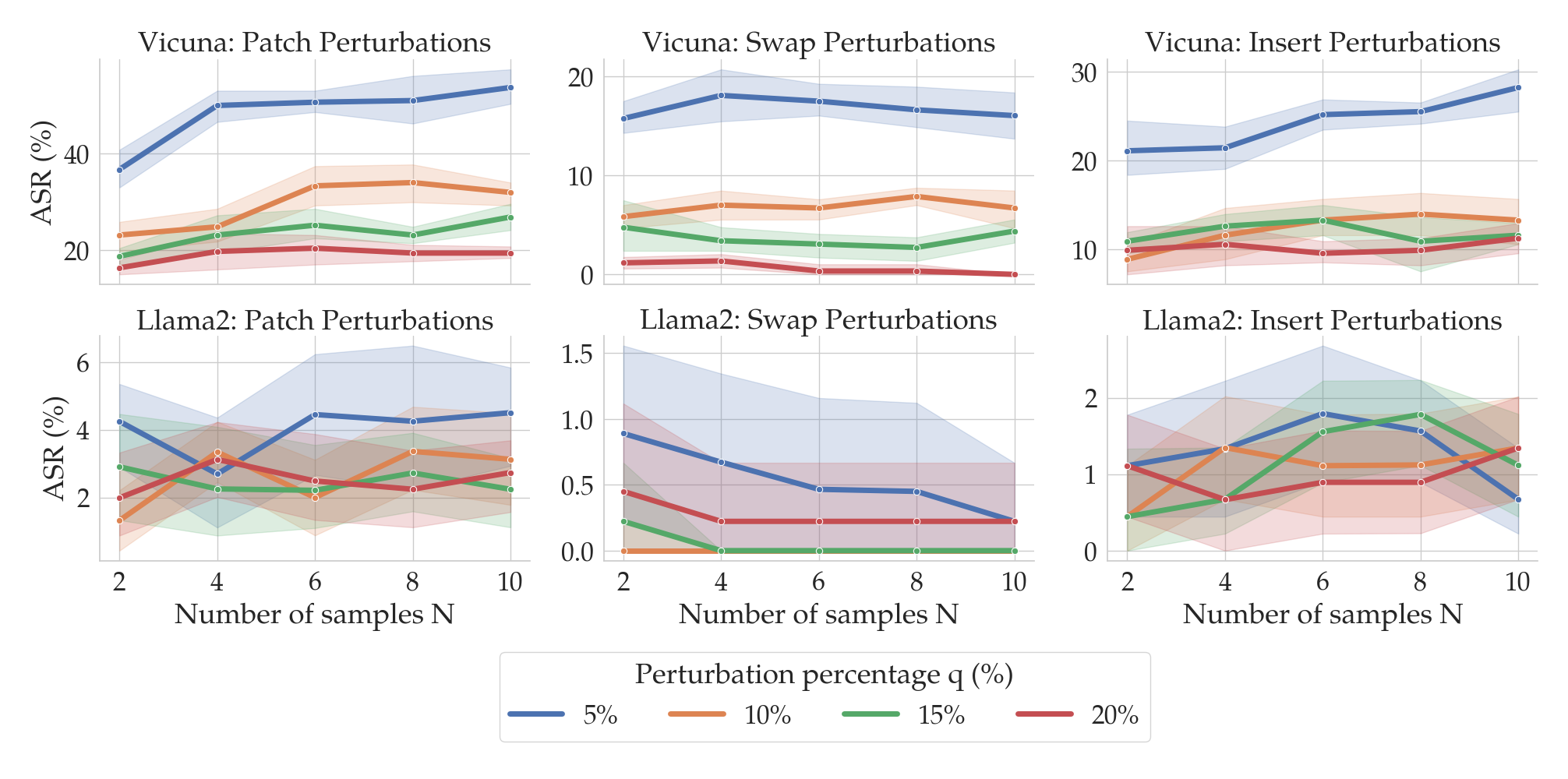
So far, we have seen that SmoothLLM is a strong defense against GCG attacks. However, a natural question is as follows: Can one design an algorithm that jailbreaks SmoothLLM? In other words, do there exist adaptive attacks that can directly attack SmoothLLM?
In our paper, we show that one cannot directly attack SmoothLLM due to GCG. The reasons for this are technical and beyond the scope of this post; the short version is that one cannot easily compute gradients of SmoothLLM. Instead, we derived a new algorithm, which we call SurrogateLLM, which adapts GCG so that it can attack SmoothLLM. We found that overall, this adaptive attack is no stronger than attacks optimized against undefended LLMs. The results of running this attack are shown below:
In this post, we provided a brief overview of attacks on language models and discussed the exciting new field surrounding LLM jailbreaks. This context set the stage for the introduction of SmoothLLM, the first algorithm for defending LLMs against jailbreaking attacks. The key idea in this approach is to randomly perturb multiple copies of each input prompt passed as input to an LLM, and to carefully aggregate the predictions of these perturbed prompts. And as demonstrated in the experiments, SmoothLLM effectively mitigates the GCG jailbreak.
If you’re interested in this line of research, please feel free to email us at arobey1@upenn.edu. And if you find this work useful in your own research please consider citing our work.
@article{robey2023smoothllm,
title={SmoothLLM: Defending Large Language Models Against Jailbreaking Attacks},
author={Robey, Alexander and Wong, Eric and Hassani, Hamed and Pappas, George J},
journal={arXiv preprint arXiv:2310.03684},
year={2023}
}
Explanation methods for machine learning models tend to not provide any formal guarantees and may not reflect the underlying decision-making process. In this post, we analyze stability as a property for reliable feature attribution methods. We show that relaxed variants of stability are guaranteed if the model is sufficiently Lipschitz smooth to the masking of features. To achieve such a model, we develop a smoothing method called Multiplicative Smoothing (MuS) and demonstrate its theoretical and practical effectiveness.
Modern machine learning models are incredibly powerful at challenging prediction tasks but notoriously black-box in their decision-making. One can therefore achieve impressive performance without fully understanding why. In domains like healthcare, finance, and law, it is not enough that the model is accurate — the model’s reasoning process must also be well-justified and explainable. In order to fully wield the power of such models while ensuring reliability and trust, a user needs accurate and insightful explanations of model behavior.
At its core, explanations of model behavior aim to accurately and succinctly describe why a decision was made, often with human comprehension as the objective. However, what constitutes the form and content of a good explanation is highly context-dependent. A good explanation varies by problem domain (e.g. medical imaging vs. chatbots), the objective function (e.g. classification vs. regression), and the intended audience (e.g. beginners vs. experts). All of these are critical factors to consider when engineering for comprehension. In this post we will focus on a popular family of explanation methods known as feature attributions and study the notion of stability as a formal guarantee.
For surveys on explanation methods in explainable AI (XAI) we refer to Burkart et al. and Nauta et al..
Feature attribution methods aim to identify the input features (e.g. pixels) most important to the prediction. Given a model and input, a feature attribution method assigns each input feature a score of its importance to the model output. Well known feature attribution methods include: gradient saliency-based (CNN models, Grad-CAM, SmoothGrad), surrogate model-based (LIME, SHAP), axiomatic approaches (Integrated Gradients, SHAP), and many others .
In this post we focus on binary-valued feature attributions, wherein the attribution scores denote the selection (\(1\) values) or exclusion (\(0\) values) of features for the final explanation.

That is, given a model \(f\) and input \(x\) that yields prediction \(y = f(x)\), a feature attribution method \(\varphi\) yields a binary vector \(\alpha = \varphi(x)\) where \(\alpha_i = 1\) if feature \(x_i\) is important for \(y\).
Although many feature attribution methods exist, it is unclear whether they serve as good explanations. In fact, there are surprisingly few papers about the formal mathematical properties of feature attributions as relevant to explanations. However, this gives us considerable freedom when studying such explanations, and we therefore begin with broader considerations about what makes a good explanation. To effectively use any explanation, the user should at minimum consider the following two questions:
Q1 concerns which inquiry this explanation is intended to resolve. In our context, binary feature attributions aim to answer: “which features are evidence of the predicted class?”, and any metric must appropriately evaluate for this. Q2 is based on the observation that one typically desires an explanation to be “reasonable”. A reasonable explanation promotes confidence as it allows one to “explain the explanation” if necessary.
We measure the quality of an explanation \(\alpha\) with the original model \(f\). In particular, we evaluate the behavior of \(f(x \odot \alpha)\), where \(\odot\) is the element-wise vector multiplication.


Because \(\alpha\) is a binary mask, this form of evaluation can be interpreted as selectively revealing features to the model. This approach is common in domains like computer vision, and indeed modern neural architectures like Vision Transformers can accurately classify even heavily masked images. In particular, it is desirable that an explanation \(\alpha\) can induce the original class, and we formalize this as the notion of consistency.
Definition. (Consistency) An explanation \(\alpha = \varphi(x)\) is consistent if \(f(x) \cong f(x \odot \alpha)\).
Here \(\cong\) means that two model outputs \(y, y'\) indicate the same class. Specifically, we consider classifier models \(f : \mathbb{R}^n \to [0,1]^m\), where the output \(y = f(x)\) is a vector in \([0,1]^m\) whose coordinates denote the confidence scores for the \(m\) classes. Two model outputs therefore satisfy \(y \cong y'\) when they are most confident on the same class.
We next consider how an explanation should behave with respect to the above quality metric. Principally, a good explanation \(\alpha = \varphi(x)\) should be strongly confident in its claims, and we express this in two properties. First, the explanation should be consistent, as introduced above in Q1. Second, the explanation should be stable: \(\alpha\) should contain enough salient features, such that including any more features does not alter the induced class.
We present stability as a desirable property because it allows for greater predictability when manipulating explanations. However, many feature attribution methods are not stable! An example of this is shown in the following.


A lack of stability is undesirable, since revealing more of the image should intuitively yield stronger evidence towards the overall prediction. Without stability, slightly modifying an explanation may induce a very different class, which suggests that \(\alpha\) is merely a plausible explanation rather than a convincing explanation. This may undermine user confidence, as a non-stable \(\alpha\) indicates a deficiency of salient features. We summarize these ideas below:
Stability Principle: once the explanatory features are selected, including more features should not induce a different class.
Our work studies stability as a property for reliable feature attributions. We introduce a smoothing method, MuS, that can provide stability guarantees on top of any existing model and feature attribution method.
In this section we formalize the aforementioned notion of stability and present a high-level description of our approach. First, our definition of stability is defined as follows.
Definition. (Stability) An explanation \(\alpha = \varphi(x)\) is stable if \(f(x \odot \alpha') \cong f(x \odot \alpha)\) for all \(\alpha' \succeq \alpha\).
For two binary vectors we write \(\alpha' \succeq \alpha\) to mean that \(\alpha'\) supersets the selected features of \(\alpha\). That is, \(\alpha' \succeq \alpha\) if and only if each \(\alpha_i ' \geq \alpha_i\). This definition of stability means that augmenting \(\alpha\) with additional features will not significantly change the confidence scores: \(\alpha\) already contains enough salient features to be a convincing explanation. However, it is a challenge to efficiently enforce stability in practice. This is because stability is defined as all \(\alpha' \succeq \alpha\), of which there are exponentially many.
In order to extract useful guarantees from the pits of computational intractability, we take the following approach:
Our stability guarantees are an important result, since, to our knowledge, stability-like guarantees such as this did not previously exist for feature attributions.
Fundamentally, Lipschitz smoothness aims to measure the change of a function in response to input perturbations. To quantify perturbations over explanations, we introduce a metric of dissimilarity that counts the differences between binary vectors:
\[\Delta (\alpha, \alpha') = \# \{i : \alpha_i \neq \alpha_i '\}\]In the context of masking inputs, Lipschitz smoothness measures the difference between \(f(x \odot \alpha)\) and \(f(x \odot \alpha')\) as a function of \(\Delta (\alpha, \alpha')\). Given a scalar \(\lambda > 0\), we say that \(f\) is \(\lambda\)-Lipschitz to the masking of features if
\[\mathsf{outputDiff}(f(x \odot \alpha), f(x \odot \alpha')) \leq \lambda \Delta (\alpha, \alpha')\]where \(\mathsf{outputDiff}\) is a metric on the classifier outputs that we detail in our paper. This Lipschitz smoothness means that the change in confidence scores from \(f(x \odot \alpha)\) to \(f(x \odot \alpha')\) is bounded by \(\lambda \Delta (\alpha, \alpha')\). Under this condition: a sufficiently small \(\lambda \Delta (\alpha, \alpha')\) can provably guarantee that \(f(x \odot \alpha) \cong f(x \odot \alpha')\). Observe that a smaller \(\lambda\) is generally desirable, as it allows one to tolerate larger deviations between \(\alpha\) and \(\alpha'\).
Lipschitz smoothness gives us the theoretical tooling to examine variants of stability for \(\alpha'\) close to \(\alpha\). In this post we consider incremental stability as one such variant, and consider others in our paper.
Definition. (Incremental Stability) An explanation \(\alpha = \varphi(x)\) is incrementally stable with radius \(r\) if \(f(x \odot \alpha') \cong f(x \odot \alpha)\) for all \(\alpha' \succeq \alpha\) where \(\Delta(\alpha, \alpha') \leq r\).
The radius \(r\) is a conservative theoretical bound on the allowable change to \(\alpha\). A radius of \(r\) means that, provably, up to \(r\) features may be added to \(\alpha\) without altering its induced class. Different inputs may have different radii, and note that we need \(r \geq 1\) to have a non-trivial incremental stability guarantee. Quantifying this radius in relation to the Lipschitz smoothness of \(f\) is one of our main results (Step 3 of The Plan), sketched below.
Theorem Sketch. (Radius of Incremental Stability) Suppose that \(f\) is \(\lambda\)-Lipschitz to the masking of features, then an explanation \(\alpha = \varphi(x)\) is incrementally stable with radius \(r = \mathsf{confidenceGap}(f(x \odot \alpha)) / (2 \lambda)\).
The \(\mathsf{confidenceGap}\) function computes the difference between the first and second highest confidence classes. A greater confidence gap indicates that \(f\) is more confident about its prediction, and that the second-best choice does not even come close.
However, the above criteria are contingent on the classifier \(f\) satisfying the relevant Lipschitz smoothness, which does not hold for most existing and popular classifiers! This thereby motivates using a smoothing method, like MuS, to impose such smoothness properties.
The goal of smoothing is to transform a base classifier \(h : \mathbb{R}^n \to [0,1]^m\) into a smoothed classifier \(f : \mathbb{R}^n \to [0,1]^m\), such that \(f\) is \(\lambda\)-Lipschitz with respect to the masking of features. This base classifier may be any classifier, e.g. ResNet, Vision Transformer, etc. Our key insight is that randomly dropping features from the input attains the desired smoothness, which we will simulate by sampling \(N\) binary masks \(s^{(1)}, \ldots, s^{(N)} \sim \mathcal{D}\). Many choices of \(\mathcal{D}\) in fact work, but one may intuit it as the \(n\)-dimensional coordinate-wise iid \(\lambda\)-parameter Bernoulli distribution \(\mathcal{B}^n(\lambda)\).
Given input \(x\) and base classifier \(h\), the evaluation of \(f(x)\) may be understood in three stages.
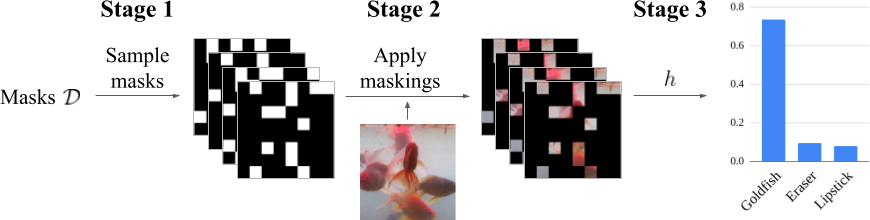
In expectation, this \(f\) is \(\lambda\)-Lipschitz with respect to the masking of features. We remark that \(\lambda\) is fixed before smoothing, and that this three-stage smoothing is applied for any input: even explanation-masked inputs like \(x = x' \odot \alpha\).
Although it is simple to view \(\mathcal{D}\) as \(\mathcal{B}^n (\lambda)\), there are multiple valid choices for \(\mathcal{D}\). In particular, it suffices that each coordinate of \(s \sim \mathcal{D}\) is marginally Bernoulli: that is, each \(s_i \sim \mathcal{B}(\lambda)\). The distribution \(\mathcal{B}^n (\lambda)\) satisfies this marginality condition, but so will others. We now present our main smoothing result.
Theorem Sketch. (MuS) Let \(s \sim \mathcal{D}\) be any random binary vector where each coordinate is marginally \(s_i \sim \mathcal{B}(\lambda)\). Consider any \(h\) and define \(f(x) = \underset{s \sim \mathcal{D}}{\mathbb{E}}\, h(x \odot s)\), then \(f\) is \(\lambda\)-Lipschitz to the masking of features.
This generic form of \(\mathcal{D}\) has strong implications for efficiently evaluating \(f\): if \(\mathcal{D}\) were coordinate-wise independent (e.g. \(\mathcal{B}^n(\lambda)\)), then one needs \(N = 2^n\) deterministic samples of \(s \sim \mathcal{D}\) to exactly compute \(f(x)\), which may be expensive. We further discuss in our paper how one can construct \(\mathcal{D}\) with statistical dependence to allow for efficient evaluations of \(f\) in \(N \ll 2^n\) samples.
To evaluate the practicality of MuS, we ask the following: can MuS obtain non-trivial guarantees in practice? We show that this is indeed the case!
Experimental Finding: MuS can achieve non-trivial guarantees on off-the-shelf feature attribution methods and classification models.
Moreover, the stability guarantees are obtained with only a light penalty to accuracy. These results of guarantees are significant, because not only are the formal properties of feature attributions not well known, there are in fact results about their limitations.
In this post we present experiments that test whether one can yield non-trivial guarantees from a popular feature attribution method, SHAP. We select the top-25% scoring features of SHAP to be our explanation method \(\varphi\), we take our classifier \(f\) to be Vision Transformer, and we sample \(N = 2000\) image inputs \(x\) from ImageNet1K. We are interested in the different qualities of guarantees obtained as one varies the smoothing parameter \(\lambda\). Below we plot the fraction of images that satisfy incremental stability (and consistency) up to some radius, where we express this radius as a fraction \(r/n\) of the total features.
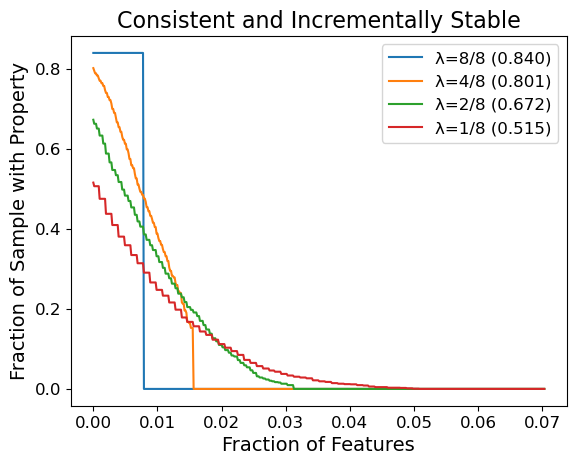
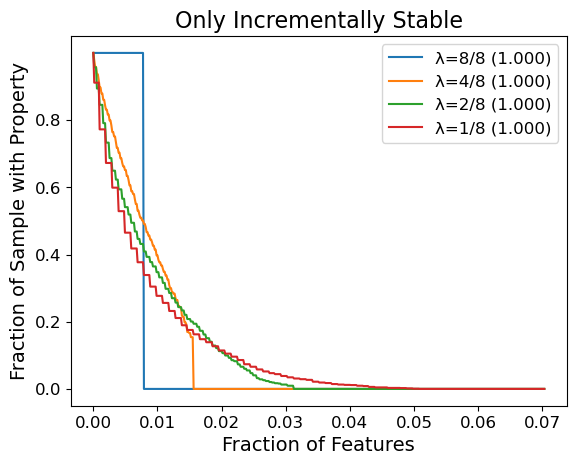
For instance with \(\lambda = 1/8\), about \(20\%\) of the samples achieve both consistency and incremental stability with radius \(\geq 1\%\) of the image (\((3 \times 224 \times 224) \times 0.01 \approx 1500\) features). If we omit the consistency requirement, then even more images achieve the same radius. To our knowledge, these are important results: prior to our work there were no formal guarantees for stability-like properties on general feature attribution methods for generic models. In addition, SHAP is not explicitly designed for stability, so it is significant that even a simple modification like top-25% selection can yield non-trivial guarantees. It is future work to investigate feature attribution methods that are better suited to maximizing such guarantees.
We remark there is an upper-bound on the radius of stability MuS can guarantee: we will always have a radius of \(r \leq 1 / (2 \lambda)\), which explains why curves for the same value of \(\lambda\) have the same zero-points. This upper-bound is because our results for smoothing requires that the classifier \(f\) be bounded, and we pick a range of \([0,1]^m\) without loss of generality. To work around this theoretical limitation, we present in our paper some parametrization strategies that allow for greater radii of stability.
Finally, we refer to our paper for a comprehensive suite of experiments that evaluate the effectiveness of MuS across vision and language models along with different feature attribution methods.
In this post we presented stability guarantees as a formal property for feature attribution methods: a selection of features is stable if the additional inclusion of other features do not alter its induced class. We showed that if the classifier is Lipschitz with respect to the masking of features, then one can guarantee incremental stability. To achieve this Lipschitz smoothness we developed a smoothing method called Multiplicative Smoothing (MuS) and analyzed its theoretical properties. We showed that MuS achieves non-trivial stability guarantees on existing feature attribution methods and classifier models.
]]>@misc{xue2023stability,
author = {Anton Xue and Rajeev Alur and Eric Wong},
title = {Stability Guarantees for Feature Attributions with Multiplicative Smoothing},
year = {2023},
eprint = {2307.05902},
archivePrefix = {arXiv},
primaryClass = {cs.LG}
}
Getting expert knowledge from domain specialists is an expensive and lengthy process. In this post, we explore how to generate domain-specific rules from the data using statistical quantiles with logic programming. This framework, which we call Statistical Quantile Rules (SQR), is capable of generating hundreds of thousands of rules that are consistent with the underlying data without a domain specialist.
Models make mistakes that stem from a variety of causes: noisy data, distribution shift, adversarial manipulation, and so on. Accuracy, the most common metric, aggregates all these errors into a single number. However, not all mistakes are created equal. While some errors may be close to correct, other errors can be nonsensical and are inconsistent with even basic rules that govern the data.
For instance, here is a figure that shows such a nonsensical error.

The green bounding box is a prediction made by the EfficientPS model, a top model for detecting objects on the self-driving CityScapes dataset. The bounding box is as wide as the street and is predicted to be a car. However, there does not exist a reasonable car that comes close to this width for its height! Even worse, this kind of error can cause the vehicle’s controller to abruptly halt to avoid the perceived danger, potentially causing harmful consequences.
These kinds of errors contradict rules based on human intuition, such as our understanding about the typical width of a car with respect to its height. In this work, we seek to generate rules that capture nonsensical errors from the data without having to rely on a domain expert. We can then use these rules to find violations as well as improve model predictions to respect these rules.
One way to find such rules is to manually craft them. This is the typical approach when creating domain-specific rules, but doing so is challenging and costly, especially at scale. An alternative approach, which we take in this work, is to appeal to the underlying data to automatically extract and generate rules.
But what makes a good rule? We can’t just generate any rule, or they might end up being nonsensical as well. A good rule should satisfy the following desiderata:
Given these three requirements, we propose to specify such rules as Statistical Quantile Rules (SQRs). An SQR is exactly what it sounds like: a rule based on the quantile statistic, which is estimated from the data.
Intuitively, this states that the interval rule $a \leq \phi(X) \leq b$ is valid for $1 - \delta$ of all the data, and thus satisfies the validity requirement when the quantile $\delta$ is sufficiently small. After picking a desired quantile $\delta$, the values of $a$ and $b$ are estimated from the data as the upper and lower $1 - \delta$ quantile bounds.
Coming back to our example, if we consider
We can estimate the interval $(a,b)$ in the SQR by calculating the aspect ratios of all the cars in the dataset, and taking the 1- and 99-percentile. This results in the rule
\[0.07 \leq \mathtt{ratio}(X) \leq 2.77\]While this rule is satisfied by 98% of all the ground truth bounding boxes of cars, it is not satisfied by the prediction from our example. We can therefore use such rules to identify predictions that violate them.
Such rules can also be made more expressive by using more complex statistics, or by even combining statistics. For instance, one can combine statistics like the widths and aspect ratios of the bounding boxes of cars to produce rules such as the follows:
\((\mathtt{ratio}(X) < 0.81 \land 20.22 \leq \mathtt{width}(X) < 1655.17) \land\) \((0.81 \leq \mathtt{ratio}(X) < 1.16 \land 14.4 \leq \mathtt{width}(X) < 614.24) \land \ldots\)
This, along with the fact that all the values are generated given a dataset and a value of $\delta$, also allows for generating several such rules at scale from a small set of statistics.
Now that we have defined SQRs, we can now try to generate them at scale. To do so, we propose the Statistical Quantile Rule Learning (SQRL) framework. SQRL is a framework that integrates logic-based methods with statistical inference to derive these rules from a model’s training data without supervision. It also allows adapting models to these rules at test time to reduce rule violations and produce more coherent predictions.
Let’s go through how SQRL works step by step, using the EfficientPS model trained on the KITTI dataset as an example. Before we can start creating SQRs, we need to figure out the relevant statistics.
We use something called a rule schema to outline the rules we want to create.

This schema, shown in the figure, details the shape of the rule, the statistics to base it on, the labels to use in the generation process, and other factors. For example, we could use a rule schema to create SQRs for the aspect ratios of cars, people, trees, and so on. For instance, we can specify a rule schema to generate SQRs over the aspect ratios of cars, people, trees, etc.
Once the rule schema is specified, we can generate the SQRs. This is a two-step process. First, we generate abstract rules that fit the shape outlined in the rule schema, as so:

Note that none of the abstract rules contain any of the statistically inferred bounds associated with the rules.
We then statistically generate the bounds for these abstract rules to produce a suite of concrete rules that make up our final set of SQRs:
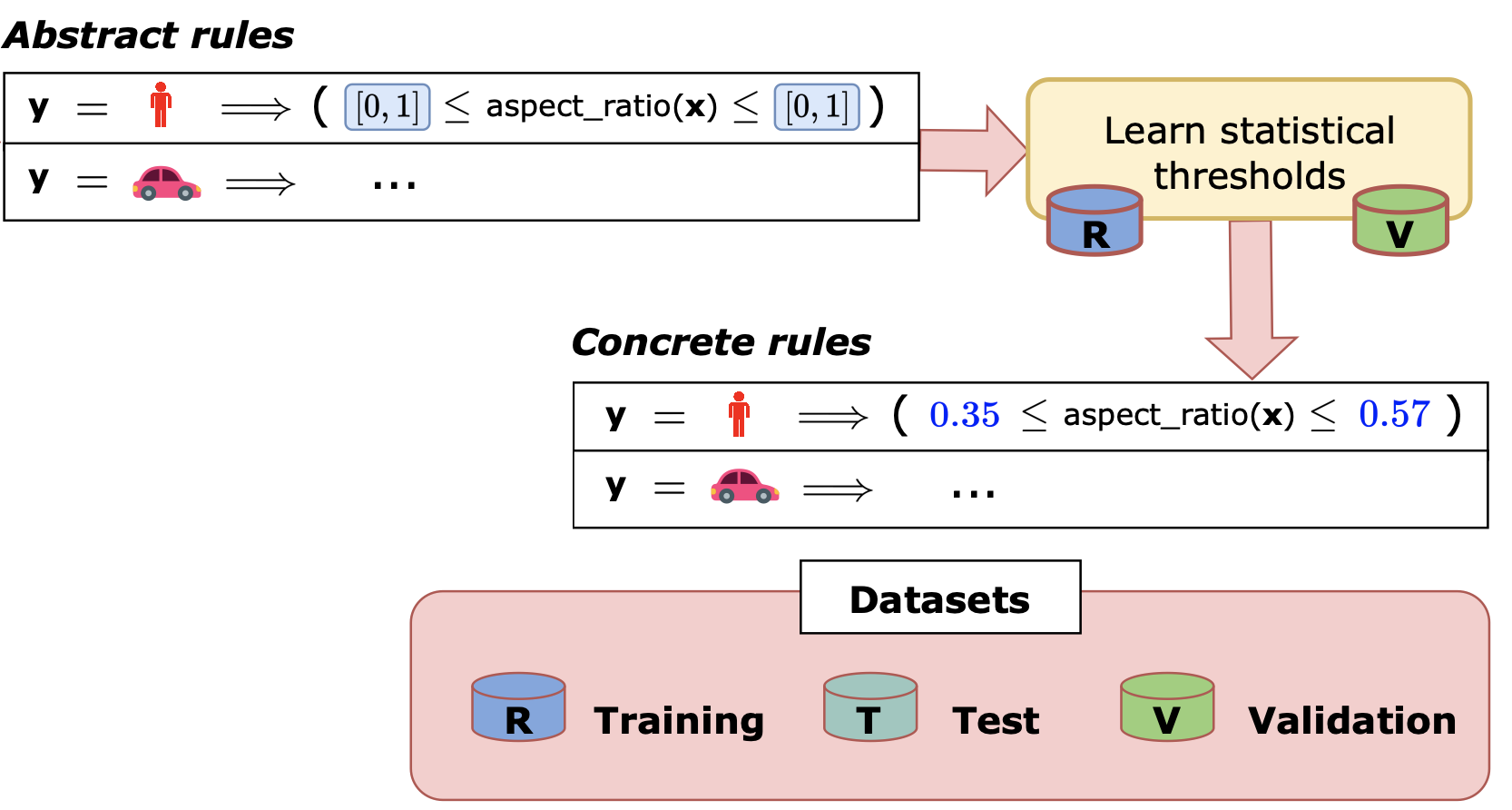
One can also optionally validate these rules using a held out validation set to consider only the most valid rules.
While there are several potential applications for SQRs, we focus on two of them in this work. We first evaluate models use the suite of generated SQRs, and then improve them by adapting them to the SQRs at test time. We study this over five applications and domains in our paper, but we will focus on three of them here.


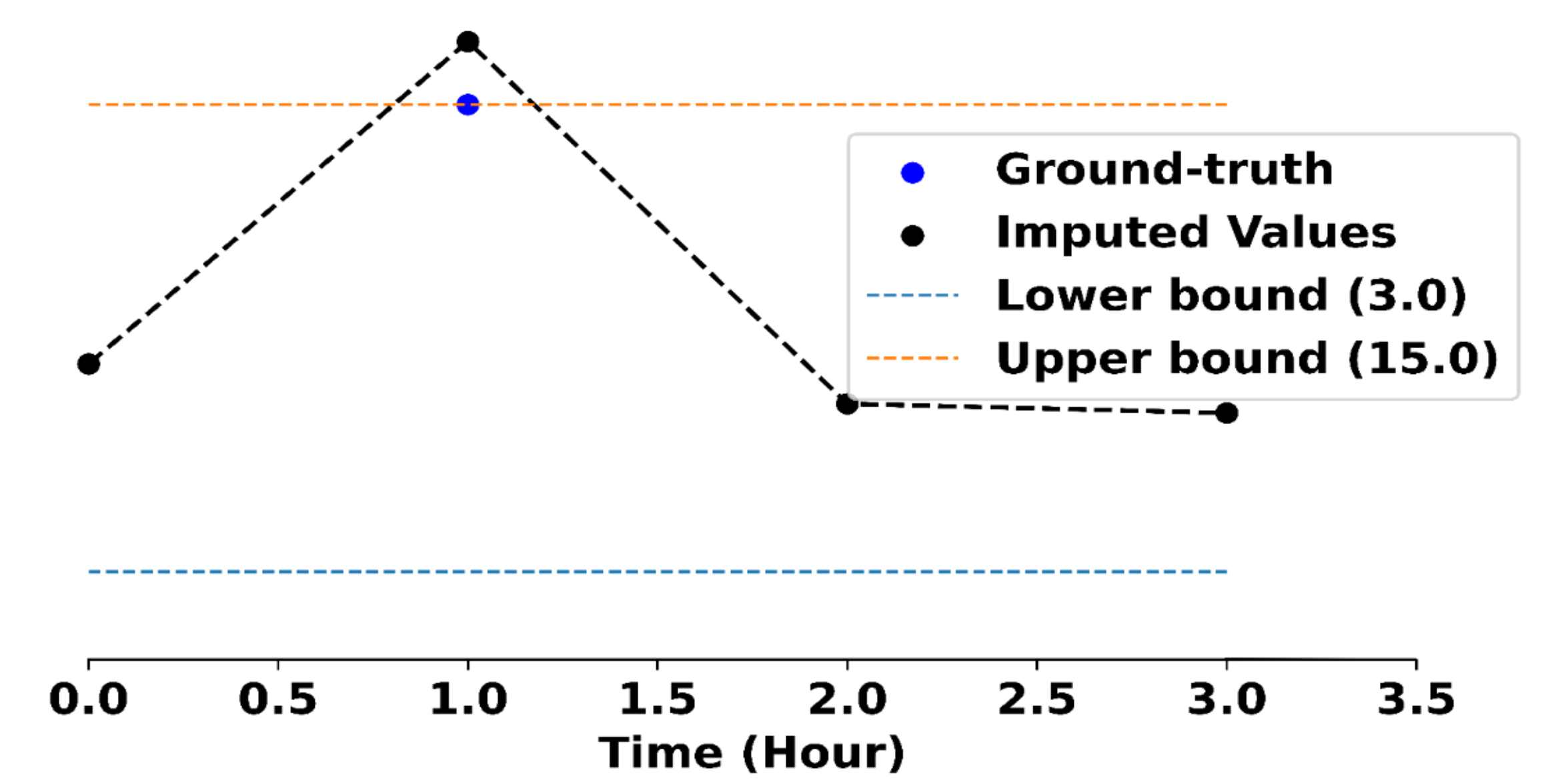

Anttila's online department store - NetAnttila - has an established position as the best-known, most visited, and most shopped online store in Finland.The rule is violated because according to the feature extraction models, the likelihood that the sentence is about fitness is 0.021, and that it is about news is 0.141, which is outside the bounds specified by the rule. However, adapting FinBert to this rule results in the prediction being changed to neutral, which is the correct sentiment for this sentence. Overall, we find a total of only 578 violations (around 0.6 violations per sample) for this task, though after adapting the model at test time to these SQRs, we find that the violations reduce by around 16%.
In conclusion, we formalized statistical quantile rules as a means of characterizing basic errors inconsistent with training data and defined the problem of extracting such rules at scale. We also proposed the SQRL framework to generate such rules and showed how to use them to evaluate and improve models. For more details, please refer to our paper here.
]]>@article{naik2023machine, title={Do Machine Learning Models Learn Statistical Rules Inferred from Data?}, author={Naik, Aaditya and Wu, Yinjun and Naik, Mayur and Wong, Eric}, year={2023} }
Complex reasoning tasks, such as commonsense reasoning and math reasoning, have long been the Achilles heel of Language Models (LMs), until a recent line of work on Chain-of-Thought (CoT) prompting [6, 7, 8, i.a.] brought striking performance gains.
In this post, we introduce a new reasoning franework, Faithful CoT, to address a key shortcoming of existing CoT-style methods – the lack of faithfulness. By guaranteeing faithfulness, our method provides a reliable explanation of how the answer is derived. Meanwhile, it outperforms vanilla CoT on 9 out of the 10 datasets from 4 diverse domains, showing a strong synergy between interpretability and accuracy.
Chain-of-Thought (CoT) prompting [7] is a type of few-shot learning technique, where an LM is prompted to generate a reasoning chain along with the answer, given only a few in-context exemplars (right). This has remarkably boosted LMs’ performance on a suite of complex reasoning tasks, compared to standard prompting [1], where the model is prompted to generate only the answer but not the reasoning chain (left).
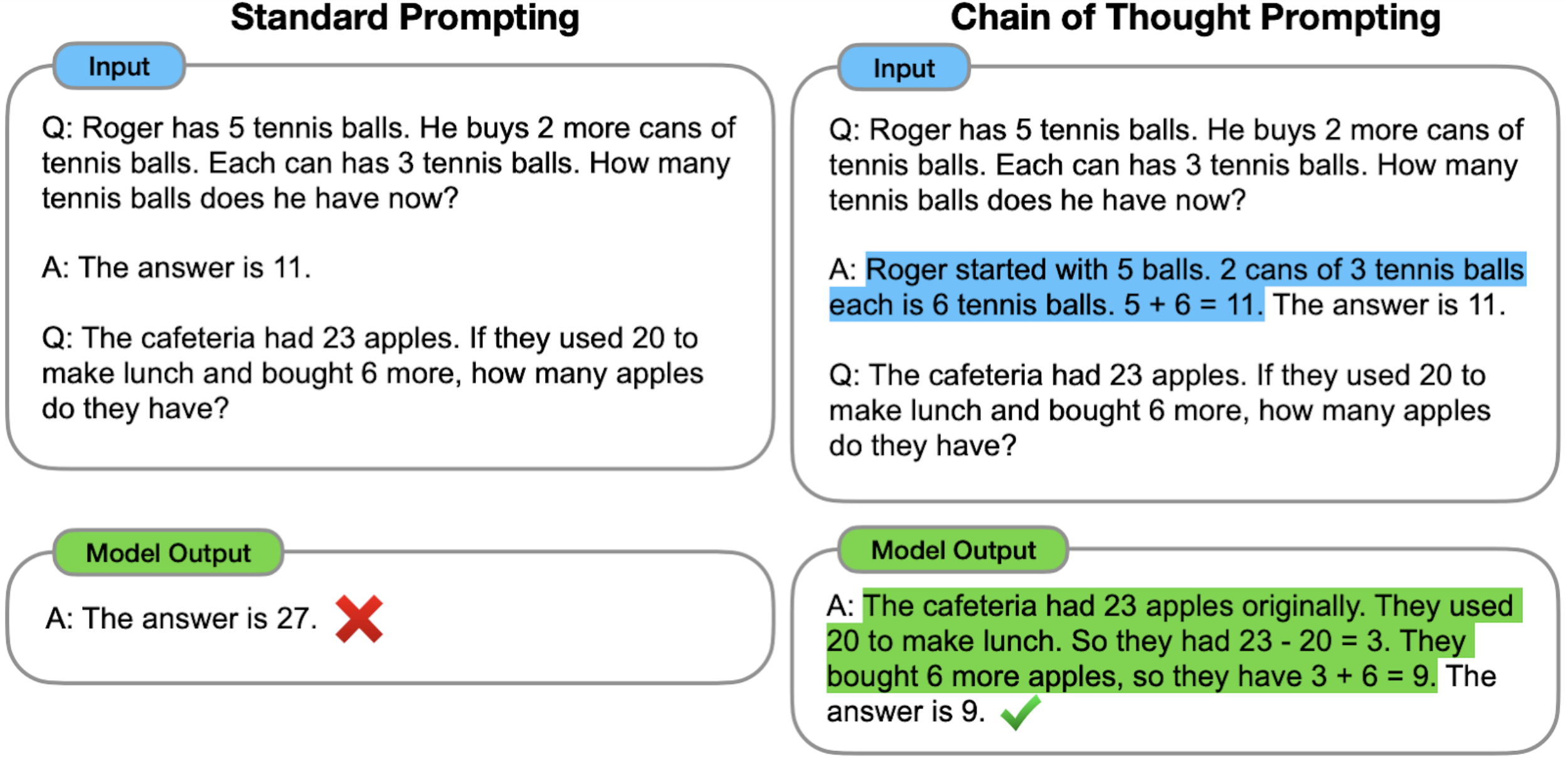
In addition to accuracy improvement, CoT is claimed to “provide an interpretable window into the behavior of the model”. But are these CoT reasoning chains actually good “explanations”?
Not necessarily, because they lack one fundamental property of interpretability, faithfulness:
Faithfulness: An explanation (e.g., the generated reasoning chain) should accurately represent the reasoning process behind the model’s prediction (i.e., how the model arrives at the final answer)”[3].
In most existing CoT-style methods, the final answer does not necessarily follow from the previously generated reasoning chain, so there is no guarantee on faithfulness:

In the above example of CoT output, the answer “0” is not even mentioned in the reasoning chain. In other words, the LM doesn’t really get to the answer in the way that it states to. This, along with more examples in our paper and other recent studies (e.g., [5]), illustrates that such CoT methods are not truely self-interpretable.
The lack of faithfulness in CoT can be dangerous in high-stake applications because it can give a false impression of “inherent interpretiblity”, whereas there is indeed no causal relationship between the reasoning chain and the answer. Even worse, when an unfaithful explanation looks plausible (i.e., convincing to humans), this makes it easier for people (e.g., legal practitioners) to over-trust the model (e.g., a recidivism predictor) even if it has implicit biases (e.g., against racial minorities) [4].
We propose Faithful CoT, a faithful-by-construction prompting framework where the answer is derived by deterministically executing the reasoning chain. Specifically, we break down a complex reasoning task into two stages: Translation and Problem Solving.
During Translation, an LM translates a Natural Language query into a reasoning chain, which interleaves Natural Language and Symbolic Language. The Natural Language component is a decomposition of the original query into multiple simpler, interdependent subproblems. Then, each subproblem is solved in a task-dependent Symbolic Language, such as Python, Datalog, or Planning Domain Definition Language (PDDL). Next, in the Problem Solving stage, the reasoning chain is executed by a deterministic solver, e.g., a Python/Datalog interpreter, or a PDDL planner, to derive the answer.
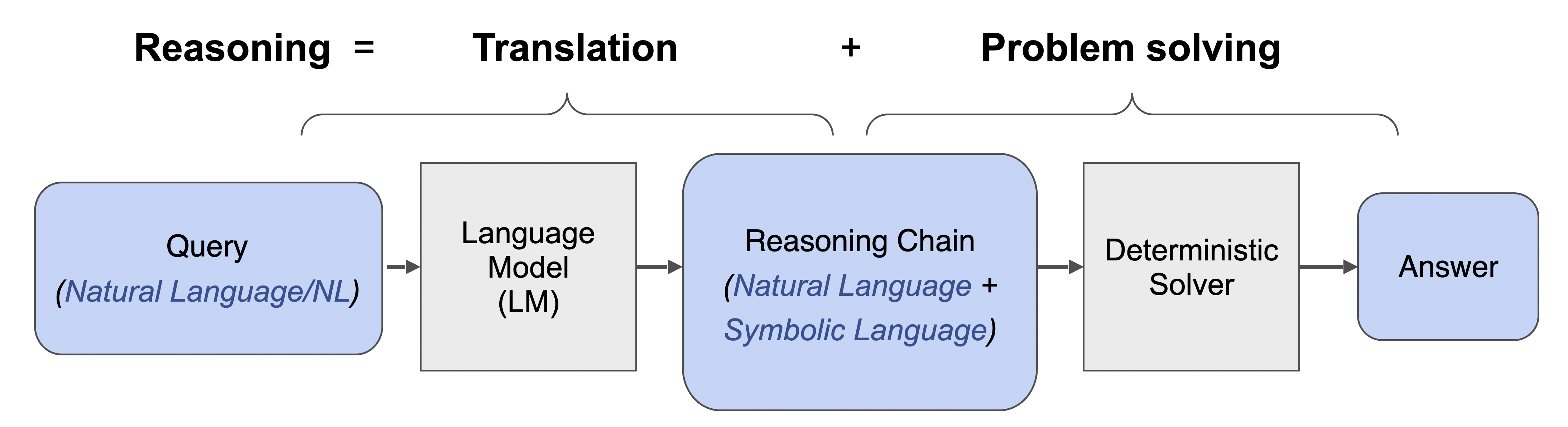
Our method is applicable to various reasoning tasks, thanks to its flexible integration with any choice of SL and external solver. We show how it works on four diverse tasks: Math, Multi-hop Question Answering (QA), Planning, and Relational Reasoning. Click the following tabs to explore each task.
Math Reasoning: Given a math question, we want to obtain the answer as a real-valued number. Here, we use Python as the symbolic language and the Python Interpreter as the determinstic solver. Below is an example from GSM8K, a dataset of grade-school math questions.

Multi-hop Question Answering (QA): The input is a question involving multiple steps of reasoning, and the answer can be True, False, or a string. Depending on the dataset, we use either Datalog or Python as the symbolic language, and their respective interpreter as the solver. Here’s an example from the StrategyQA dataset, which contains open-domain science questions.

Planning: In a user-robot interaction scenario, the user gives a household task query, and the goal is come up with a plan of actions that the robot should take in order to accomplish the task. The symbolic language we use for this scenario is Planning Domain Definition Language (PDDL), a standard encoding language for classical planning tasks. Then, we use a PDDL planner as the solver. See an example from the Saycan dataset, consisting of user queries in a kitchen scenario.

Relational Reasoning: Given a relational reasoning problem, we want to obtain the answer as a string variable. For example, the CLUTRR dataset involves inferring the family relationship between two people from a short story. Here, we use logical expressions as the symbolic language and a simple rule-based inference engine as the solver. See the following example.

Though our key motivation is to enhance interpretability, we do find that faithfulness empirically improves LMs’ performance on various reasoning tasks. We show this on 10 datasets from the four domains above: Math Reasoning (GSM8K, SVAMP, MultiArith, ASDiv, AQUA), Multi-hop QA (StrategyQA, Date Understanding, Sports Understanding), Planning (Saycan), and Logical Inference (CLUTRR).
In comparison with existing prompting methods (standard [1], CoT [7], Least-to-Most [8]), Faithful CoT performs the best on 8 out of the 10 datasets, with the same underlying LM (code-davinci-002) and greedy decoding strategy. In particular, Faithful CoT outperforms CoT with an average accuracy gain of 4.5 on MWP, 1.9 on Planning, 4.2 on Multi-hop QA, and 18.1 on Logical Inference. This performance gain generalizes across multiple code-generation LMs (code-davinci-001, code-davinci-002, text-davinci-001, text-davinci-002, text-davinci-003, gpt-4; see our repo for latest results).
As for the other two datasets, Faithful CoT and Least-to-Most prompting both perform almost perfectly (99+ accuracy) on Sports Understanding, which may already be saturated. On StrategyQA, there is still a large accuracy gap between Faithful CoT and other methods. The primary cause is likely the sparsity of Datalog in the pretraining data for Codex, which we exmaine with an in-depth analysis in our paper. Still, with further pretraining on Datalog, we believe that there is room for improvement with our method.
After the recent release of ChatGPT (gpt-3.5-turbo) and GPT-4 (gpt-4) were released, we also experiment with them as the underlying LM Translator, instead of Codex:
| Math Reasoning | Planning | Multi-hop QA | Relational Reasoning | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GSM8K | SVAMP | MultiArith | ASDiv | AQUA | saycan | StrategyQA | date | sports | CLUTRR | |
| Codex | 72.2 | 83.5 | 98.8 | 80.2 | 47.2 | 89.3 | 63.0 | 81.6 | 99.1 | 58.9 |
| ChatGPT | 75.8 | 83.0 | 95.3 | 81.7 | 53.5 | 80.6 | 51.5 | 73.5 | 52.3 | 12.1 |
| GPT-4 | 95.0 | 95.3 | 98.5 | 95.6 | 73.6 | 92.2 | 54.0 | 95.8 | 99.3 | 62.7 |
Notably, equipped with GPT-4, Faithful CoT sets the new State-of-the-Art performance on many of the above datasets, achieving 95.0+ few-shot accuracy (❗) on almost all Math Reasoning datasets, Date Understanding, and Sports Understanding. However, the gap on StrategyQA becomes even larger.
How sensitive is Faithful CoT to various design choices in the prompt, such as the choice of exemplars and the phrasing of the prompt? To answer this, we vary each factor and repeat the experiment for multiple times (see our paper for details).
The above results show that the performance gains of Faithful CoT are minimally influenced by these factors, suggesting the robustness of our method.
How much does each component of Faithful CoT contribute to the performance? We perform an ablation study where we remove different parts from the framework and see how the performance changes. In addition to the original prompt (Full), we experiment with four variations:
No rationale: we remove the rationales in the prompt, i.e., everything in the brackets from the NL comments, e.g., independent, support: ["There are 15 trees"].
No NL but nudge: we remove all NL comments in the prompt except the “nudge” line: e.g., # To answer this question, we write a Python program to answer the following subquestions.
No NL: we remove all NL comments in the prompt.
No solver: Instead of calling the external solver, we add Answer: {answer} to the end of every exemplar and let the LM predict the answer itself.
The external solver turns out to be essential to the performance, as it relieves the burden of problem solving from the LM. Without it, the accuracy suffers a huge decline on GSM8K, Date Understanding, and CLUTRR (-50.8, -22.9, and -19.4 respectively), while on SayCan it improves by 2.9 nonetheless, potentially because of its data homogeneity (see further analysis in our paper).
We’ve introduced Faithful CoT, a novel framework that addresses the lack of faithfulness in existing CoT-style prompting methods. By splitting the reasoning task into two stages, Translation and Problem Solving, our framework provides a faithful explanation of how the answer is derived, and additionally improves the performance across various reasoning tasks and LMs.
For more details, check out our paper and Github repository.
Concurrent with our work, Chen et al. (2022) [2] and Gao et al. (2022) [3] also explore the similar idea of generating programs as reasoning chains. We recommend that you check out their cool work as well!
[1] Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., … & Amodei, D. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33, 1877-1901.
[2] Chen, W., Ma, X., Wang, X., & Cohen, W. W. (2022). Program of thoughts prompting: Disentangling computation from reasoning for numerical reasoning tasks. arXiv preprint arXiv:2211.12588.
[3] Gao, L., Madaan, A., Zhou, S., Alon, U., Liu, P., Yang, Y., … & Neubig, G. (2023, July). Pal: Program-aided language models. In International Conference on Machine Learning (pp. 10764-10799). PMLR.
[4] Slack, D., Hilgard, S., Jia, E., Singh, S., & Lakkaraju, H. (2020, February). Fooling lime and shap: Adversarial attacks on post hoc explanation methods. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society (pp. 180-186).
[5] Turpin, M., Michael, J., Perez, E., & Bowman, S. R. (2023). Language Models Don’t Always Say What They Think: Unfaithful Explanations in Chain-of-Thought Prompting. arXiv preprint arXiv:2305.04388.
[6] Wang, X., Wei, J., Schuurmans, D., Le, Q. V., Chi, E. H., Narang, S., … & Zhou, D. (2022, September). Self-Consistency Improves Chain of Thought Reasoning in Language Models. In The Eleventh International Conference on Learning Representations.
[7] Wei, J., Wang, X., Schuurmans, D., Bosma, M., Xia, F., Chi, E., … & Zhou, D. (2022). Chain-of-thought prompting elicits reasoning in large language models. Advances in Neural Information Processing Systems, 35, 24824-24837.
[8] Zhou, D., Schärli, N., Hou, L., Wei, J., Scales, N., Wang, X., … & Chi, E. H. (2022, September). Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. In The Eleventh International Conference on Learning Representations.
@article{lyu2023faithful,
title={Faithful Chain-of-Thought Reasoning},
author={Lyu, Qing and Havaldar, Shreya and Stein, Adam and Zhang, Li and Rao, Delip and Wong, Eric and Apidianaki, Marianna and Callison-Burch, Chris},
journal={arXiv preprint arXiv:2301.13379},
year={2023}
}
Large language models have recently enabled a prompting based, few-shot learning paradigm referred to as in-context learning (ICL). However, the ICL paradigm can be quite sensitive to small differences in the input prompt, such as the template of the prompt or the specific examples chosen. To handle this variability, we leverage the framework of influences to select which examples to use in a prompt. These so-called in-context influences directly quantify the performance gain/loss when including a specific example in the prompt, enabling improved and more stable ICL performance.
Prompting is a recent interface for interacting with general-purpose large language models (LLMs). Instead of fine-tuning an LLM on a specific task and dataset, users can describe their needs in natural language in the form of a “prompt” to guide the LLM towards all kinds of task. For example, LLMs have been asked to write computer programs, take standardized exams, or even come up with original Thanksgiving dinner recipes.
To elicit better performance, the research community has identified techniques for prompting LLMs. For example, providing detailed instructions or asking the model to think step-by-step can help direct it to make more accurate predictions. Another way to provide guidance is to give the model examples of input-output pairs before asking for a new prediction. In this work, we focus on this last approach to prompting often referred to as few-shot in-context learning (ICL).
In-context learning involves providing the model with a small set of high-quality examples (few-shot) via a prompt, followed by generating predictions on new examples.
As an example, consider GPT-3, a general-purpose LLM that takes prompts as inputs. We can instruct GPT-3 to do sentiment analysis via the following prompt.
This prompt contains 3 examples of review-answer pairs for sentiment analysis (3-shot), which are the in-context examples.
We would like to classify a new review, My Biryani can be a tad spicier, as either positive or negative.
We append the input to the end of our in-context examples:
Review: The butter chicken is so creamy.
Answer: Positive
Review: Service is subpar.
Answer: Negative
Review: Love their happy hours
Answer: Positive
Review: My Biryani can be a tad spicier.
Answer:Negative
To classify the final sentence, we have given this prompt as input to GPT-3 to generate a completion. We simply consider the probability of the model generating the word Negative versus the word Positive, and use the higher-probability word (conditional on the examples) as the prediction.
In this case, it turns out that the model can correctly predict Negative as being a more likely completion than Positive.
Note that in this example, we were able to adapt the LLM to do sentiment analysis with no parameter updates to the model. In the fine-tuning paradigm, doing a similar task would often require more human-annotated data and extra training.
ICL allows general-purpose LLMs to adapt to new tasks without training. This lowers the sample complexity and the computational cost of repurposing the model. However, these benefits also come with drawbacks. In particular, the performance of ICL can be susceptible to various design decision when constructing prompts. For example, the natural language template used to format a prompt, the specific examples included in the prompt, and even the order of examples can all affect how well ICL performs [ACL tutorial].
In other words, ICL is brittle to small changes in the prompt. Consider the previous prompt that we gave to GPT-3, but suppose we instead swap the order of the first two examples:
Review: Service is subpar.
Answer: Negative
Review: The butter chicken is so creamy.
Answer: Positive
Review: Love their happy hours
Answer: Positive
Review: My Biryani can be a tad spicier.
Answer:Positive
When given this adjusted prompt, the model’s prediction changes and is now incorrectly predicting a positive sentiment! Why did this happen? It turns that in-context learning suffers from what is known as recency bias. Specifically, recent examples tend to have a larger impact on the model’s prediction. Since the model recently saw two positive examples, it spuriously followed this label pattern when making a new prediction. This behavior makes ICL unreliable—the performance should not be dependent on a random permutation of examples in the prompt!
To address this unreliability, we look towards a variety of methods that aim to quantify and understand how training data affects model performance. For example, Data Shapley values and influence functions both aim to measure how much an example affects performance when included in the training dataset. Inspired by these frameworks, our goal is to measure how much an in-context example affects ICL performance when included in the prompt. In particular, we will calculate the influence of each potential example on ICL performance, which we call in-context influences.
More formally, let \(S\) be a training set and \(f(S)\) be the validation performance after training on \(S\). We calculate in-context influences with a two-step process:
\[ {\mathcal{I}(x_j)=\frac{1}{N_j}\sum_{S_i:x_j\in S_i} f(S_i)} - {\frac{1}{M-N_j}\sum_{S_i:x_j\notin S_i} f(S_i)} \]
where \(M\) is the number of total subsets used to estimate influences, \(N_j\) is the total number of subsets containing example \(x_j\), and \(f(S_i)\) is the performance metric when evaluated on the validation set.\(^1\)
In other words, a higher score for \(\mathcal{I}(x_j)\) corresponds to a higher average improvement in validation performance when \(x_j\) was included in the prompt. This is analogous to the meaning of influences in the classic setting, but adapted to the ICL setting: instead of training models on a dataset, we are prompting models on examples.
In the following figure, we visualize the distribution of computed influences of training examples on ICL performance.
The two tails of the influence distribution identify highly impactful in-context examples. Examples with large positive influence tend to help ICL performance, whereas examples with large negative influence tend to hurt ICL performance. This observation suggests a natural approach for creating prompts for ICL: we can use examples in the right tail to create the “best” prompt, or use examples from the left tail to create the “worst” performing prompt.
\(^1\)This method of estimating influences with random subsets has similarities to the framework of datamodels, which uses random subsets to train a linear model that predicts performance. In our paper, we also consider a similar analog of the datamodels approach for estimating in-context influences.
Once we have computed in-context influences, we can use these influences to select examples for ICL. Intuitively, examples with more positive influences should lead to better ICL performance. As a sanity check, is this indeed the case?
In the following figure, we partition the training data into 10 percentile bins according to their influence scores, and measure the validation performance of prompts using examples from each bin.
We find a steady and consistent trend: examples with higher influences do in fact result in higher test performance in most models and tasks! Interestingly, we find a significant difference between examples with positive and negative influences: a 22.2% difference on the task WSC and 21.5% difference on the task WIC when top-bin examples are used instead of bottom-bin examples on OPT-30B. This provides one explanation for why the choice of examples can drastically affect ICL performance: according to our influence calculations, there exists a small set of training examples (the top and bottom influential examples) that have a disproportionate impact on ICL performance.
Classic influences have found qualitatively that positively influencial examples tend to be copies of examples from the validation set, while negatively influential examples tend to be mislabeled or noisy examples. Do influences for ICL also show similar trends?
We find that in some cases, these trends also carry over to the ICL setting. For example, here is a negatively influential examples in the PIQA task:
Goal: flashlight
Answer: shines a light
In this case, the example is quite unnatural for the task: rather than flashlight being a goal for shining a light, it would be more natural to have shining a light be a goal for the flashlight. This is an example of how the design of the template can result in poor results for certain input-output pairs. This is especially true when the template is not universally suitable for all examples in the training data.
However, in general we found that differences between examples with positive or negative influences was not always immediately obvious (more examples are in our paper). Although we can separate examples into bins corresponding to positive and negative influence, identifying the underlying factors that resulted in better or worse ICL performance remains an open problem!
In this blog post, we propose a simple influence-based example selection method that can robustly identify low- and high- performing examples. Our framework can quantify the marginal contribution of an example as well as different phenomena associated with ICL, such as the positional biases of examples.
For more details and additional experiments (ablation studies, case studies on recency bias, and comparisons to baselines) please check out our paper and code.
Concurrent to our work, Chang and Jia (2023) also employ influences to study in-context learning. They show the efficacy of influence-based selection on many non-SuperGLUE tasks. You can check out their work here.
]]>@article{nguyen2023incontextinfluences,
author = {Nguyen, Tai and Wong, Eric},
title = {In-context Example Selection with Influences}, journal = {arXiv},
year = {2023},
}