Stability guarantees are an emerging tool for understanding how reliable explanations are. However, current methods rely on specialized architectures and give guarantees that are too conservative to be useful. To address these limitations, we introduce soft stability and propose a simple, sample-efficient stability certification algorithm (SCA) that can flexibly work with any model and give more useful guarantees. Our guarantees are orders of magnitude greater than existing methods and can scale to be usable in practice in high-dimensional settings.
Powerful machine learning models are increasingly deployed in real-world applications. However, their opacity poses a significant challenge to safety, especially in high-stakes settings where interpretability is critical for decision-making. A common approach to explaining these models is through feature attributions methods, which highlight the input features that contribute most to a prediction. However, these explanations that are the selected features are often brittle, as shown in the following figure.

Sea Turtle

Sea Turtle ✓

Coral Reef ✗
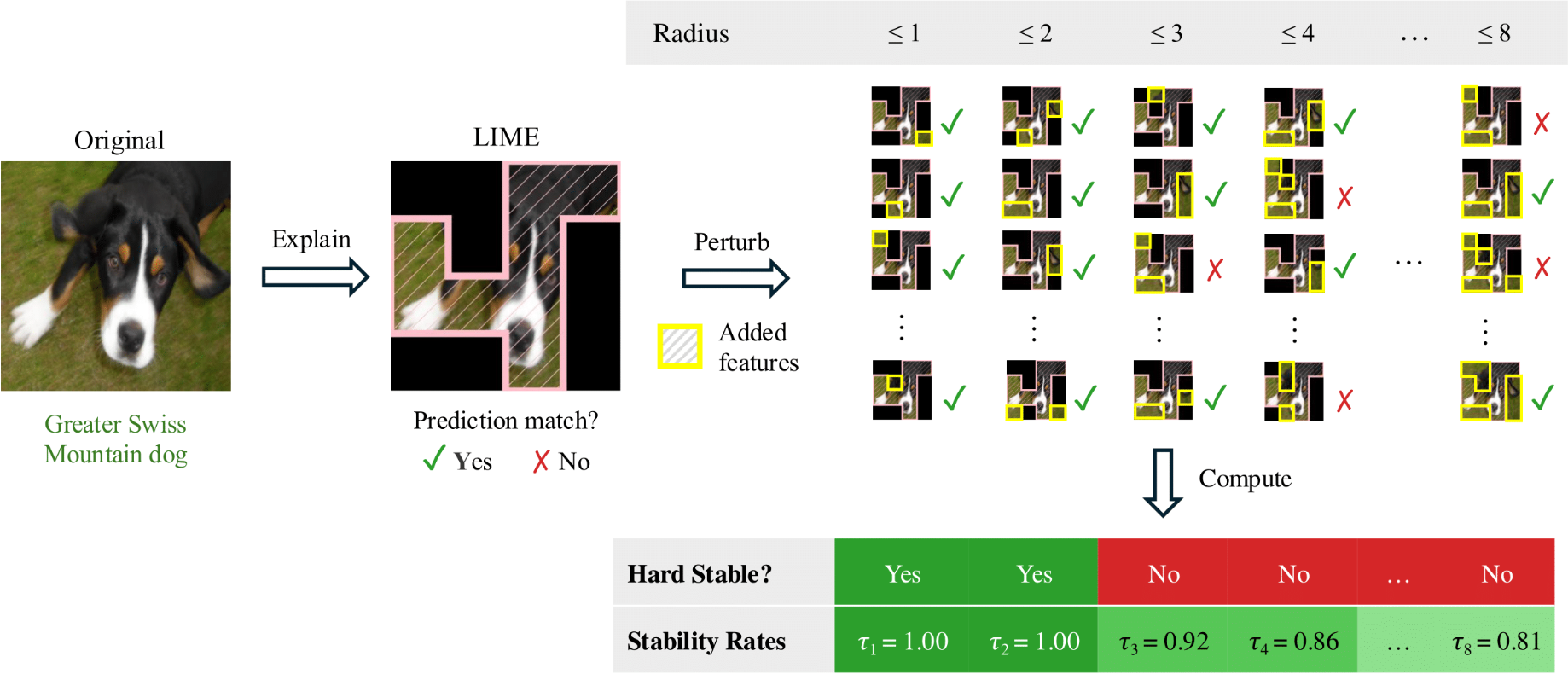
An ideal explanation should be robust: if a subset of features is genuinely explanatory for the prediction, then revealing any small set of additional features should not change the prediction, up to some tolerance threshold. This is the notion of hard stability, which was explored in a previous blog post.
As it turns out, finding this tolerance exactly is non-trivial and computationally intractable. A first approach was the MuS algorithmic framework, which multiplicatively smooths models to have nice mathematically properties that enable efficiently lower-bounding the maximum tolerance. However, there are still significant drawbacks:
- Reliance on specialized architectures, in particular smoothed classifiers, constrain their applicability.
- The resulting guarantees are overly conservative, meaning they certify only small perturbations, limiting practical use.
In this work, we address these limitations and introduce soft stability, a new form of stability with mathematical and algorithmic benefits that outweigh those of hard stability. We also introduce the Stability Certification Algorithm (SCA), a simpler model-agnostic, sampling-based approach for certifying both hard and soft stabilities with rigorous statistical guarantees.
Soft stability: a more flexible and scalable guarantee
In the figure below, we give a high-level overview of the core idea behind stability (both hard and soft variants). That is, stability measures how an explanation’s prediction changes as more features are revealed.
Although both hard stability and soft stability describe how predictions change as features are revealed, the fundamental difference lies in how they measure robustness. We compare and contrast their definitions below.
We use “radius” to refer to the perturbation size, i.e., the number of features added, following robustness conventions. This radius is also used as part of soft stability’s definition. But rather than measuring whether the prediction is always preserved, soft stability instead measures how often it is preserved.
The stability rate provides a fine-grained measure of an explanation’s robustness. For example, two explanations may appear similar, but could in fact have very different levels of robustness.

 $\tau_2 = 0.37$ ✗
$\tau_2 = 0.37$ ✗
 $\tau_2 = 0.76$ ✓
$\tau_2 = 0.76$ ✓
By shifting to a probabilistic perspective, soft stability offers a more refined view of explanation robustness. Two key benefits follow:
- Model-agnostic certification: The soft stability rate is efficiently computable for any classifier, whereas hard stability is only easy to certify for smoothed classifers.
- Practical guarantees: The certificates for soft stability are much larger and more practically useful than those obtained from hard stability.
Certifying soft stability: challenges and algorithms
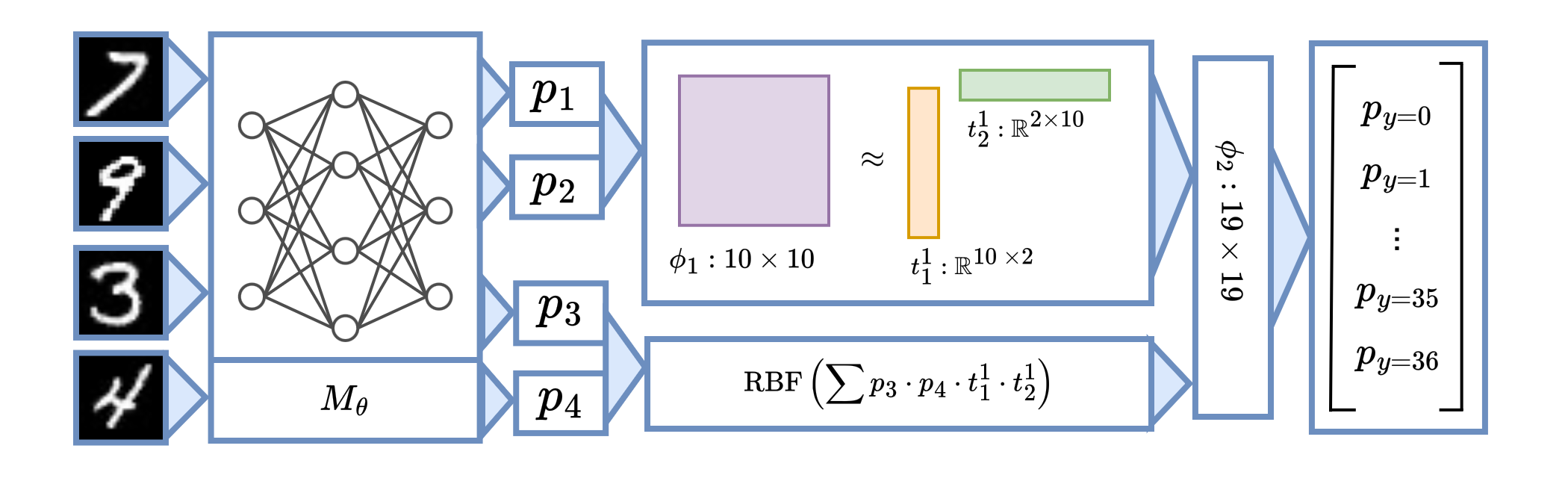
At first, certifying soft stability (computing the stability rate) appears daunting. If there are $m$ possible features that may be included at radius $r$, then there are $\mathcal{O}(m^r)$ many perturbations to check! In fact, this combinatorial explosion is the same computational bottleneck encountered when one tries to naively certify hard stability.
Fortunately, we can efficiently estimate the stability rate to a high accuracy using standard sampling techniques from statistics. This procedure is summarized in the following figure.
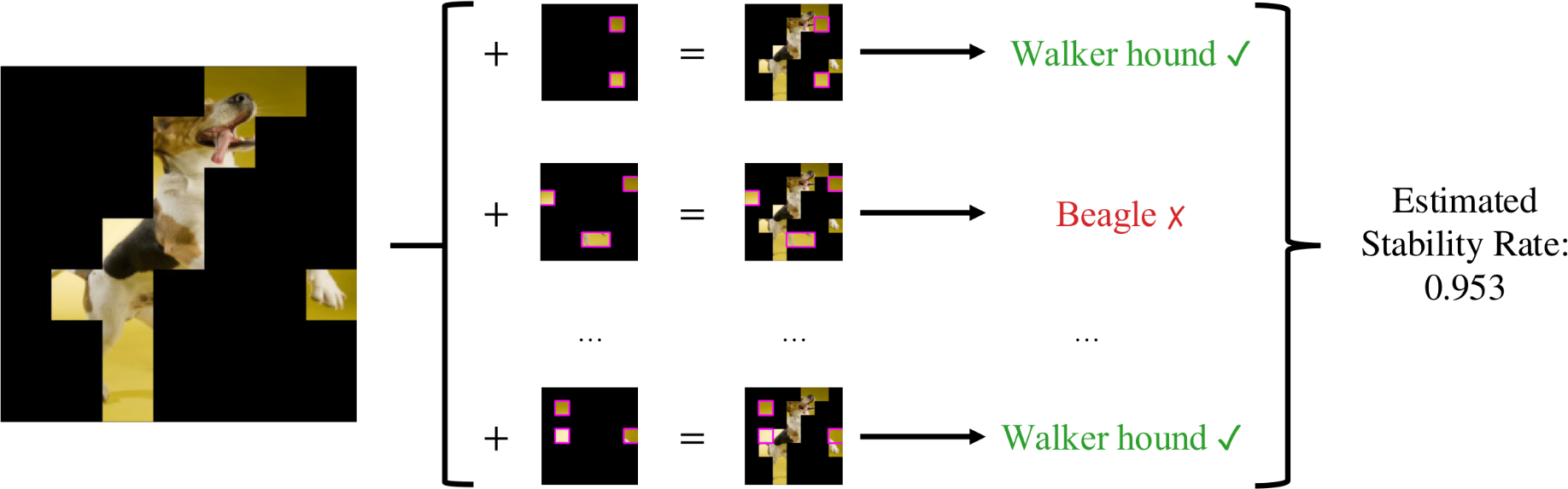
We outline this estimation process in more detail below.
We can compute an estimator $\hat{\tau}_r$ in the following manner:
2. Let $\hat{\tau}_r$ be the fraction of the samples whose predictions match the original explanation's prediction.
We also give a reference implementation in our tutorial notebook.
There are three main benefits of estimating stability in this manner. First, SCA is model-agnostic, which means that soft stability can be certified for any model, not just smoothed ones — in contrast to hard stability. Second, SCA is sample-efficient: the number of samples depends only on the hyperparameters $\varepsilon$ and $\delta$, meaning that the runtime cost scales linearly with the cost of running the classifier. Thirdly, as we show next, soft stability certificates from SCA are much less conservative than those obtained from MuS, making them more practical for giving fine-grained and meaningful measures of explanation robustness.
Experiments
We next evaluate the advantages of stability certification algorithm (SCA) over MuS, a prior existing certification method for feature attributions. We also study how stability guarantees vary across vision and language tasks, as well as across different explanation methods.
We first show that soft stability certificates obtained through SCA are stronger than those obtained from MuS, which quickly becomes vacuous as the perturbation size grows. The graphs below are for Vision Transformer model over $2000$ samples from ImageNet, and RoBERTa model over TweetEval, and explanation method LIME, where we select the top-25% ranked features as the explanation.
We also show the stability rates attainable with a Vision Transformer model over $1000$ samples from ImageNet using different explanation methods.
For each method, we select the top-25% ranked features as the explanation.
On the right, we show the stability rates we can attain on RoBERTa and TweetEval.
For more details on other models and experiments, please refer to our paper.
Mild smoothing improves soft stability
Should we completely abandon smoothing? Not necessarily! Although the algorithm for certifying does not require a smoothed classifier, we empirically found that mildly smoothed models often have empirically improved stability rates. Moreover, we can explain these empirical observations using techniques from Boolean function analysis.
Click for details
The particular smoothing implementation we consider involves randomly masking (i.e., dropping, zeroing) features, which we define as follows.
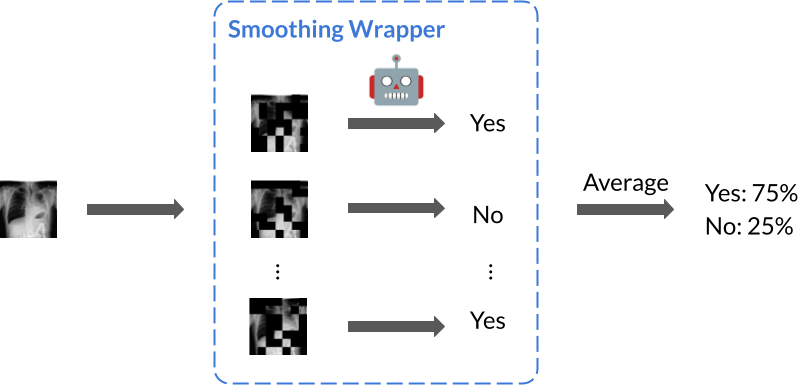
Definition. [Random Masking] For an input $x \in \mathbb{R}^d$ and classifier $f: \mathbb{R}^d \to \mathbb{R}^m$, define the smoothed classifier as $\tilde{f}(x) = \mathbb{E}_{\tilde{x}} f(\tilde{x})$, where independently for each feature $x_i$, the smoothed feature is $\tilde{x}_i = x_i$ with probability $\lambda$, and $\tilde{x}_i = 0$ with probability $1 - \lambda$. That is, a smaller $\lambda$ means stronger smoothing.
In the original context of certifying hard stability, this was also referred to as multiplicative smoothing because the noise scales the input. One can think of the smoothing parameter $\lambda$ as the probability that any given feature is kept, i.e., each feature is randomly masked (zeroed, dropped) with probability $1 - \lambda$. Smoothing becomes stronger as $\lambda$ shrinks: at $\lambda = 1$, no smoothing occurs because $\tilde{x} = x$ always; at $\lambda = 1/2$, half the features of $x$ are zeroed out on average; at $\lambda = 0$, the classifier predicts on an entirely zeroed input because $\tilde{x} = 0_d$.
Importantly, we observe that smoothed classifiers can have improved soft stability, particularly for weaker models! Below, we show examples for ViT and ResNet50.
To study the relation between smoothing and stability rate, we use tools from Boolean function analysis.
Our main theoretical finding is as follows.
Main Result. Smoothing improves the lower bound on the stability rate by shrinking its gap to 1 by a factor of $\lambda$.
In more detail, for any fixed input-explanation pair, the stability rate of any classifier $f$ and the stability rate of its smoothed variant $\tilde{f}$ have the following relationship:
\[1 - Q \leq \tau_r (f) \,\, \implies\,\, 1 - \lambda Q \leq \tau_r (\tilde{f}),\]where $Q$ is a quantity that depends on $f$ (specifically, its Boolean spectrum) and the distance to the decision boundary.
Although this result is on a lower bound, it aligns with our empirical observation that smoothed classifiers tend to be more stable. Interestingly, we found it challenging to bound this improvement using standard techniques. This motivated us to develop novel theoretical tooling, which we leave the details and experiments for in the paper.
Conclusion
In this blog post, we explore a practical variant of stability guarantees that improves upon existing methods in the literature.
For more details, please check out our paper, code, and tutorial.
Thank you for reading! Please cite if you find our work helpful.
@article{jin2025probabilistic,
title={Probabilistic Stability Guarantees for Feature Attributions},
author={Jin, Helen and Xue, Anton and You, Weiqiu and Goel, Surbhi and Wong, Eric},
journal={arXiv preprint arXiv:2504.13787},
year={2025},
url={https://arxiv.org/abs/2504.13787}
}