Concept-based interpretability represents human-interpretable concepts such as “white bird” and “small bird” as vectors in the embedding space of a deep network. But do these concepts really compose together? It turns out that existing methods find concepts that behave unintuitively when combined. To address this, we propose Compositional Concept Extraction (CCE), a new concept learning approach that encourages concepts that linearly compose.
To describe something complicated we often rely on explanations using simpler components. For instance, a small white bird can be described by separately describing what small birds and white birds look like. This is the principle of compositionality at work!


+


=


Concept-based explanations [Kim et. al., Yuksekgonul et. al.] aim to map these human-interpretable concepts such as “small bird” and “white bird” to the features learned by deep networks. For example, in the above figure, we visualize the “white bird” and “small bird” concepts discovered in the hidden representations from CLIP using a PCA-based approach on a dataset of bird images. The “white bird” concept is close to birds that are indeed white, while the “small bird” concept indeed captures small birds. However, the composition of these two PCA-based concepts results in a concept depicted in the above figure on the right which is not close to small and white birds.
Composition of the “white bird” and “small bird” concepts is expected to look like the following figure. The “white bird” concept is close to white bird images, the “small bird” concept is close to small bird images, and the composition of the two concepts is indeed close to images of small white birds!




size: 3-5in


We achieve this by first understanding the properties of compositional concepts in the embedding space of deep networks and then proposing a method to discover such concepts.
Compositional Concept Representations
To understand concept compositionality, we first need a definition of concepts. Abstractly, the concept “small bird” is nothing more than the symbols used to type it. Therefore, we define a concept as a set of symbols.
A concept representation maps between the symbolic form of the concept, such as \(``\text{small bird"}\), into a vector in a deep network’s embedding space. A concept representation is denoted \(R: \mathbb{C}\rightarrow\mathbb{R}^d\) where \(\mathbb{C}\) is the set of all concept names and \(\mathbb{R}^d\) is an embedding space with dimension \(d\).
To compose concepts, we take the union of their set-based representation. For instance, \(``\text{small bird"} \cup ``\text{white bird"} = ``\text{small white bird"}\). Concept representations, on the other hand, compose through vector addition. Therefore, we define compositional concept representations to mean concept representations which compose through addition whenever their corresponding concepts compose through the union, or that:
Definition: For concepts \(c_i, c_j \in \mathbb{C}\), the concept representation \(R: \mathbb{C}\rightarrow\mathbb{R}^d\) is compositional if for some \(w_{c_i}, w_{c_j}\in \mathbb{R}^+\), \(R(c_i \cup c_j) = w_{c_i}R(c_i) + w_{c_j}R(c_j)\).
Why Don’t Traditional Concepts Compose?
Traditional concepts don’t compose since existing concept learning methods over or under constrain concept representation orthogonality. For instance, PCA requires all concept representations to be orthogonal while methods such as ACE from Ghorbani et. al. place no restrictions on concept orthogonality.
We discover the expected orthogonality structure of concept representations using a dataset where each sample is annotated with concept names (we know some \(c_i\)’s) and we study the representation of the concepts (the \(R(c_i)\)’s). We create such a setting by subsetting the bird data from CUB to only contain birds of three colors (black, brown, or white) and three sizes (small, medium, or large) according to the dataset’s finegrained annotations.
Each image now contains a bird annotated as exactly one size and one color, so we derive ground truth concept representations for the bird shape and size concepts. To do so, we center all the representations, and we define the ground truth representation for a concept similar to existing work as the mean representation of all samples annotated with the concept.
Our main finding from analyzing the ground truth concept representations for each bird size and color (6 total concepts) is that CLIP encodes concepts of different attributes (colors vs. sizes) as orthogonal, but that concepts of the same attribute (e.g. different colors) need not be orthogonal. We make this empirical observation from the cosine similarities between all pairs of ground truth concepts, shown below.
Observation: The concept pairs of the same attribute have non-zero cosine similarity, while cross-attribute pairs have close to zero cosine similarity, implying orthogonality.
While the ground truth concept representations display this orthogonality structure, must all compositional concept representations mimick this structure? In our paper, we prove the answer is yes in a simplified setting!
Given these findings, we next outline our method for finding compositional concepts which follow this orthogonality structure.
Compositional Concept Extraction
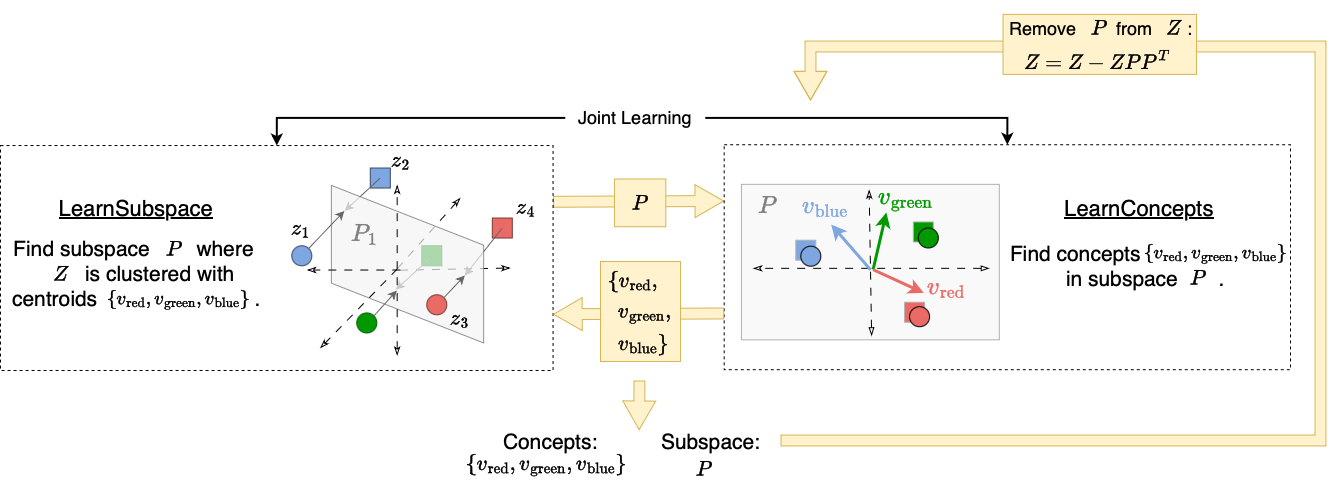
Our findings from the synthetic experiments show that compositional concepts are represented such that different attributes are orthogonal while concepts of the same attribute may not be orthogonal. To create this structure, we use an unsupervised iterative orthogonal projection approach.
First, orthogonality between groups of concepts is enforced through orthogonal projection. Once we find one set of concept representations (which may correspond to different values of an attribute such as different colors) we project away the subspace which they span from the model’s embedding space so that all further discovered concepts are orthogonal to the concepts within the subspace.
To find the concepts within a subspace, we jointly learn a subspace (with LearnSubspace) and a set of concepts (with LearnConcepts). The figure above illustrates the high level algorithm. Given a subspace \(P\), the LearnConcepts step finds a set of concepts within \(P\) which are well clustered. On the other hand, the LearnSubspace step is given a set of concept representations and tries to find an optimal subspace in which the given concepts are maximally clustered. Since these steps are mutually dependent, we jointly learn both the subspace \(P\) and the concepts within the subspace.
The full algorithm operates by finding a subspace and concepts within the subspace, then projecting away the subspace from the model’s embedding space and repeating. All subspaces are therefore mutually orthogonal, but the concepts within one subspace may not be orthogonal, as desired.
Discovering New Compositional Concepts
We qualitatively show that on larger-scale datasets, CCE discovers compositional concepts. Click through the below visualizations for examples of the disovered concepts on image and language data.
For a dataset of bird images (CUB):
For a dataset of text newsgroup postings:
-
Text Ending in "..."SportsSports text ending in "..."
Hopefully, he doesn't take it personal...
Hi there, maybe you can help me...
+If I were Pat Burns I'd throw in the towel. The wings dominated every aspect of the game.
Quebec dominated Habs for first 2 periods and only Roy kept this one from being rout, although he did blow 2nd goal.
=Grant Fuhr has done this to a lot better coaches than Brian Sutter...
No, although since the Lavalliere weirdness, nothing would really surprise me. Jeff King is currently in the top 10 in the league in *walks*. Something is up...
Discovered concepts from the Newsgroups dataset. The "Text ending in ..." concept is close to text which all ends in "...", the "Sports" concept is close to articles about sports, and the compostion of these concepts is close to samples about sports that end in "...". -
Asking for suggestionsItems for saleAsking for purchasing suggestions
HELP!
I am trying to find software that will allow COM port redirection [...] Can anyone out their make a suggestion or recommend something.Hi all,
I am looking for a new oscilloscope [...] and would like suggestions on a low-priced source for them.+Please reply to the seller below.
For Sale:
Sun SCSI-2 Host Adapter Assembly [...]Please reply to the seller below.
210M Formatted SCSI Hard Disk 3.5" [...]=Which would YOU choose, and why?
Like lots of people, I'd really like to increase my data transfer rate fromHi all,
I am looking for a new oscilloscope [...] and would like suggestions on a low-priced source for them.Discovered concepts from the Newsgroups dataset. The "Asking for suggestions" concept is close to text where someone asks others for suggestions, the "Items for sale" concept is close to ads which are listing items available for purchase, and the compostion of these concepts is close to samples where someone asks for suggestions about purchasing a new item.
CCE also finds concepts which are quantitatively compositional. Compositionality scores for all baselines and CCE are shown below for the CUB dataset as well as two other datasets, where smaller scores mean greater compositionality. CCE discovers the most compositional concepts compared to existing methods.
CCE Concepts Improve Downstream Classification Accuracy
Do the concepts discovered by CCE improve downstream classification accuracy compared to baseline methods? We find that CCE does improve accuracy, as shown below on the CUB dataset when using 100 concepts.
In the paper, we show that CCE also improves classification performance on three other datasets spanning vision and language.
Conclusion
Compositionality is a desired property of concept representations as human-interpretable concepts are often compositional, but we show that existing concept learning methods do not always learn concept representations which compose through addition. After studying the representation of concepts in a synthetic setting we find two salient properties of compositional concept representations, and we propose a concept learning method, CCE, which leverages our insights to learn compositional concepts. CCE finds more compositional concepts than existing techniques, results in better downstream accuracy, and even discovers new compositional concepts as shown through our qualitative examples.
Check out the details in our paper here! Our code is available here, and you can easily apply CCE to your own dataset or adapt our code to create new concept learning methods.