Large language models (LLM) often make reasoning errors. However, current LLM-based error detection methods often fail to detect propagated errors because earlier errors can corrupt downstream judgments. To address this, we introduce Autoregressive Reasoning Entailment Stability (ARES), an algorithmic framework for measuring reasoning soundness with statistical guarantees. ARES can reliably detect errors in long reasoning chains, especially propagated errors that other methods fail to catch.
When LLM reasoning goes wrong, there are several different failure modes. For example:
(hidden)
The denominator of a fraction is 7 less than 3 times the numerator.
If the fraction is equivalent to 2/5, what is the numerator?
- Let the numerator be x
- The denominator is 3x − 7
- So x / (3x − 7) = 2/5
- Therefore, 5x = 6x − 14
- Finally, we get x = 14 ✓
- Let the numerator be x
- The denominator is 3x − 7
-
So x / (3x − 7) = 3/5
Ungrounded -
Therefore, 5x = 9x − 20
Invalid -
Finally, we get x = 5
Propagated
As illustrated in the example above, one type of error is an ungrounded error — a step that is incorrect with respect to the given context. For example, the model might incorrectly copy a 2/5 in the context to be 3/5. Another common error is an invalid derivation — for example, deriving $5x=9x-20$ from $x/(3x-7)=3/5$ — which is a logical misstep or miscalculation. A third type of error involves error propagation: even if the logic is valid, an incorrect starting assumption can lead to a wrong conclusion. For instance, using the incorrect claim $5x=9x-20$ to derive $x=5$ is logically valid but the derived claim is incorrect due to the initial error. All of these errors are unsound claims that undermine the soundness of a reasoning chain.
Current error detection methods, such as LLM judges and Process Reward Models, typically aim to identify all errors at once. However, an LLM attempting to detect all errors with a single call is often unreliable as it can be distracted by unsound information in other steps.
To address these limitations, we introduce Autoregressive Reasoning Entailment Stability (ARES), an LLM-based framework for automated error detection. Our main idea is to certify a reasoning chain step-by-step: the soundness of successive claims are inductively computed from the stability of prior claims. Theoretically, we show that this approach admits strong yet sample-efficient statistical guarantees. Empirically, we excel where prior methods fall short, particularly in catching propagated errors within very long reasoning chains.
The Challenge of Using LLMs to Verify Reasoning
Using a large language model (LLM) to reliably determine the soundness of a reasoning chain presents several challenges.
A naive approach might be to ask an LLM to judge each step as either sound or unsound. However, this method is prone to failure. Consider the incorrect chain from our example: an LLM might be misled by step 4 (“Therefore, 5x = 9x − 20”) when evaluating step 5 (“Finally, we get x = 5”). The model could correctly see that step 5 logically follows from step 4, but fail to recognize that step 5 is ultimately unsound because it relies on an unsound premise.
This demonstrates that simple, holistic judgments with a single LLM call are insufficient. A more principled method is needed, perhaps one that uses an entailment model to check each step using only a specific subset of information, rather than the entire context.
Detecting Reasoning Errors with an Entailment Model
An entailment model determines whether a hypothesis logically follows from a premise (entailment) or whether the opposite of the hypothesis follows from the premise (contradiction). When verifying a reasoning step, we have several options for selecting the premise: we can use all previous claims leading up to the current step, only the base claims from the original context, or check whether the current claim contradicts each previous claim individually.
However, each approach has fundamental limitations. Using all previous claims as the premise suffers from error propagation: if any earlier claim is unsound, we incorporate incorrect information into subsequent verification steps and can erroneously say the unsound steps are sound — the same issue that arises when using an LLM to judge all steps holistically.
What if we restrict ourselves to only the base claims as premises? After all, these are sound claims provided in the context. This approach fails when the current step depends on a long chain of intermediate reasoning. Single-step entailment checking is insufficient; we need the sound information derived from prior inferences.
Other methods, such as ROSCOE and ReCEval, check whether the current claim contradicts any previous claim through pairwise comparison. However, this approach also risks using unsound premises and can miss errors when multiple claims must be considered together to properly evaluate the current step.
In summary, current LLM- and entailment-model-based methods are unreliable for verifying claims in reasoning chains because they fail to use all necessary sound information while simultaneously excluding unsound information.
Error Detection with ARES
To address these limitations, we pair step-by-step reasoning with step-by-step certification, proposing Autoregressive Reasoning Entailment Stability (ARES).
We first define a reasoning chain as a sequence of base claims $(C_1, \dots, C_n)$ that are given in the context, followed by derived claims $(C_{n+1},\dots,C_{n+m})$ generated by an LLM. A probabilistic entailment model $\mathcal{E}(P, H) \mapsto r$ estimates the probability that a premise $P$ entails a hypothesis $H$, where $r\in[0,1]$.
ARES assigns a stability score $\tau_k$ to each derived claim $C_{n+k}$. This score represents the expected entailment of $C_{n+k}$ by marginalizing over all $2^{n+k-1}$ possible subsets of preceding claims:
\[\tau_{k} = \sum_{\alpha \in \{0,1\}^{n+k-1}} \mathcal{E}(C(\alpha), C_{n+k}) \cdot \Pr[\alpha]\]where the binary vector $\alpha \in {0, 1}^{n+k-1}$ indicates which claims to include ($\alpha_i = 1$) or exclude ($\alpha_i = 0$) in the premise.
The probability of each premise combination, $\Pr[\alpha]$, is calculated autoregressively:
- For base claims, it is the product of their prior soundness probabilities $p_i$: \(\Pr[\alpha_{1:n}] = \prod_{i = 1}^{n} p_i^{\alpha_i} (1 - p_i)^{1-\alpha_i}\)
- For derived claims, the probability is updated inductively via the chain rule, conditioned on the entailment of each new claim: \(\Pr[\alpha_{1:n+k}] = \Pr[\alpha_{1:n+k-1}] \cdot \mathcal{E}(C(\alpha_{1:n+k-1}), C_{n+k})^{\alpha_{n+k}}\)
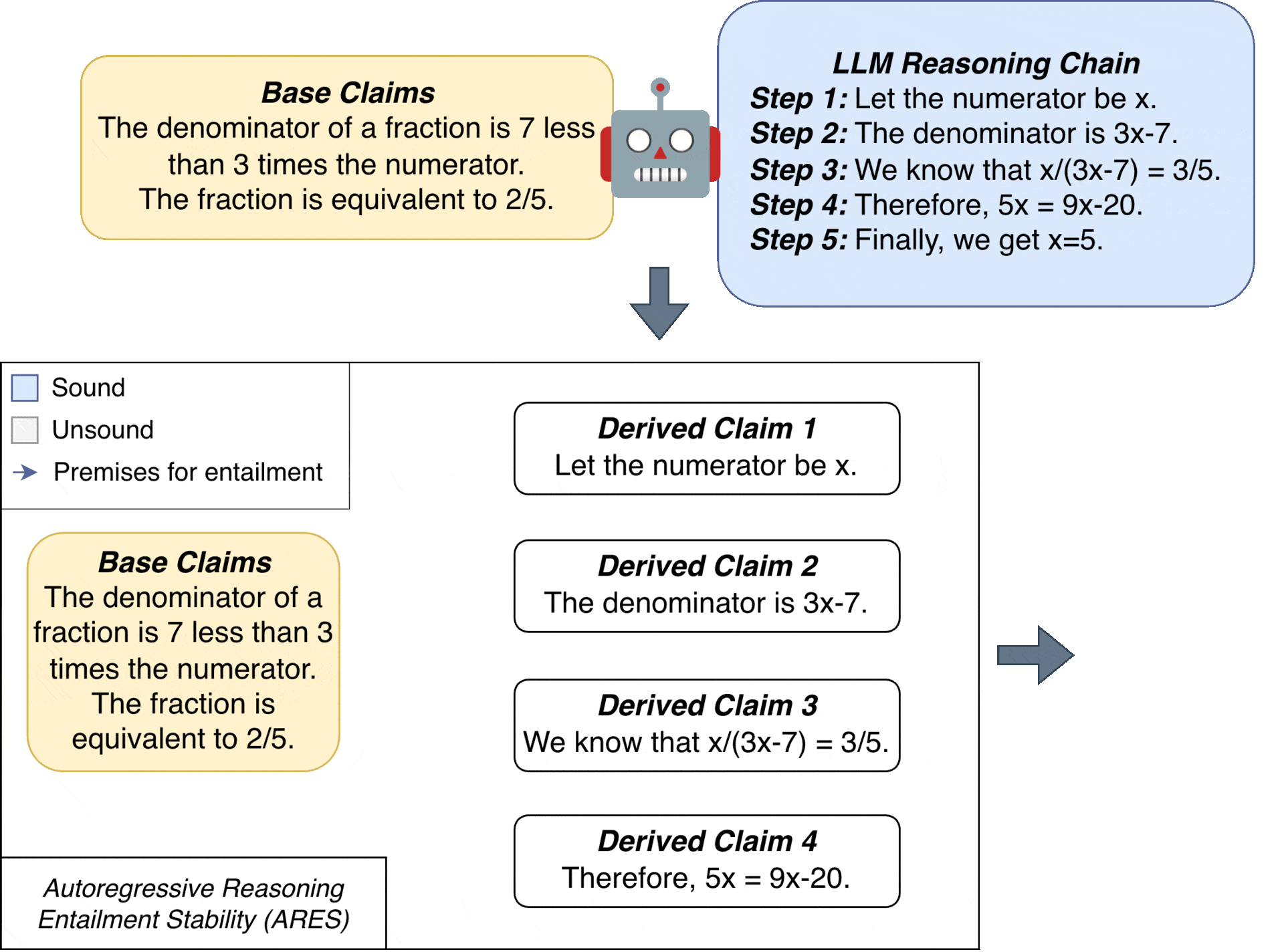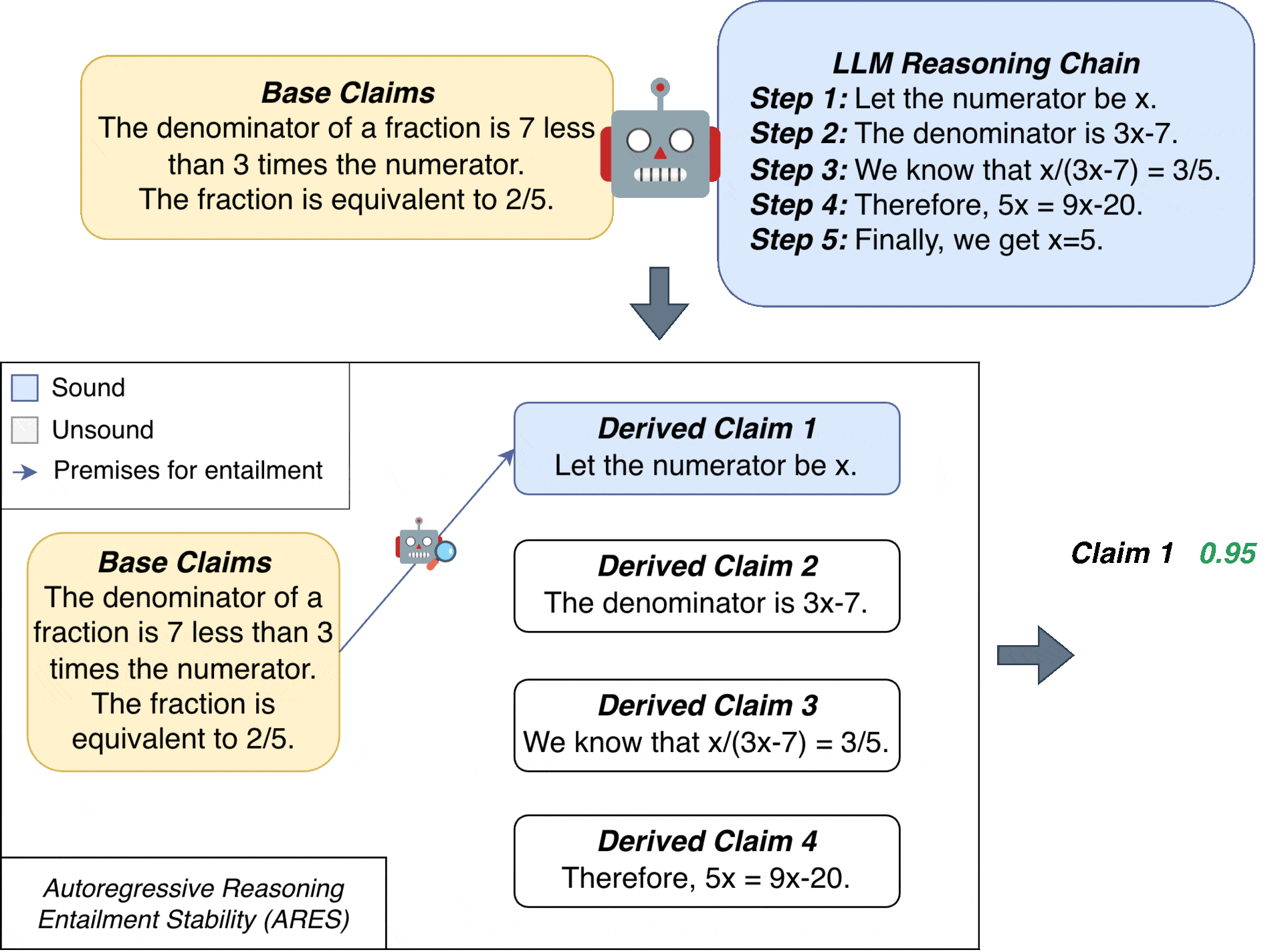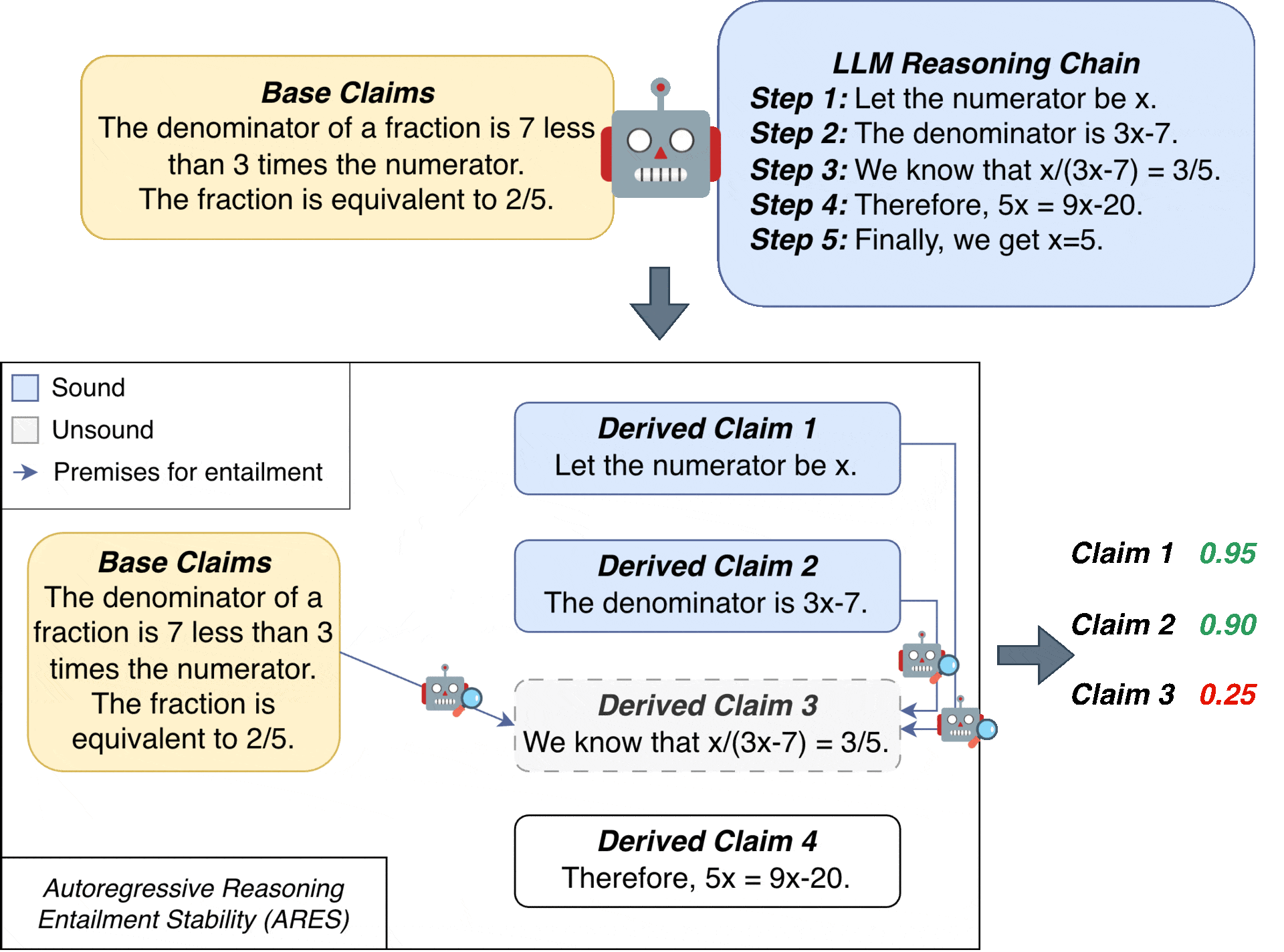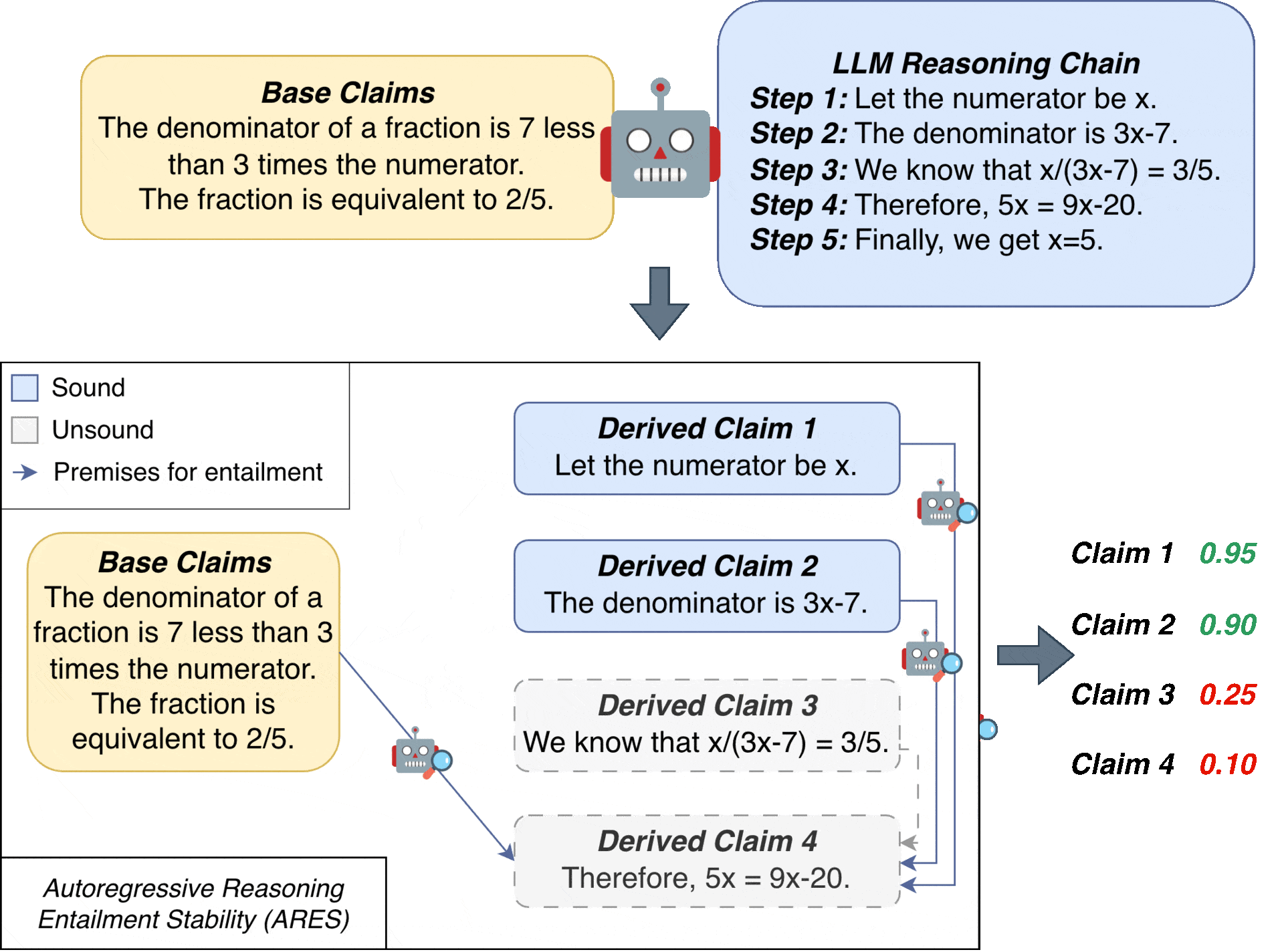
The key idea behind ARES is to evaluate each derived claim by considering all subsets of previous claims as potential premises, weighted by their probability of being sound.
Certifying probabilistic soundness via efficient sampling
The above definition of soundness is convenient to define, but it is intractable to compute! In the absence of additional problem structure, one must exhaustively enumerate over exponentially many configurations of premise inclusion-exclusions.
While exact computation is difficult, our previous work shows that we can efficiently certify stability in feature attributions to a high accuracy. The main idea is to sample a bunch of sub-reasoning chains, and then do a weighted average based on each sub-chain’s likelihood. This is illustrated in the following algorthm.
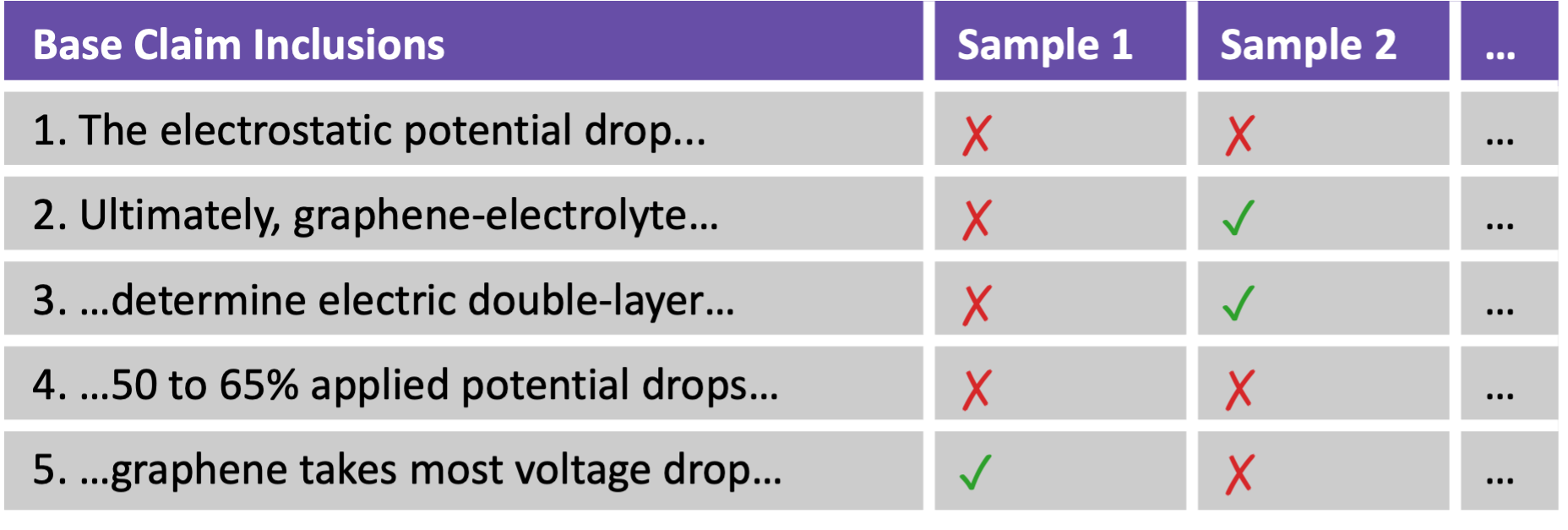
Suppose the reasoning chain consists of base claims $(C_1, \ldots, C_n)$ and derived claims $(C_{n+1}, \ldots, C_{n+m})$. We can estimate ARES score $\tau_k$ for each derived claim in a reasoning chain inductively using an entailment model instantiated from an LLM.
Draw $N$ i.i.d. random subsets, including each base claim $C_i, \ldots, C_n$ with probability $p_i$.
Step 2. For each derived claim $C_{n+k}$ ($k=1\!:\!m$):
(b) Average entailment probabilities over $N$ samples to estimate $C_{n+k}$’s stability rate $\tau_k$.
(c) For each sample $i$, include $C_{n+k}$ for certifying future steps with probability $p_{n+k}^{(i)}$.
(d) Repeat until all derived claims are evaluated.
This algorithm is illustrated in the following example. Step 1: We randomly sample inclusion of base claims based on prior probabilities for $N$ samples.
Step 2: We then iteratively compute the estimated soundness for each step.
(a) Every time, for each sample, we use the previously included claims as premise to compute the entailment rate of the next claim.
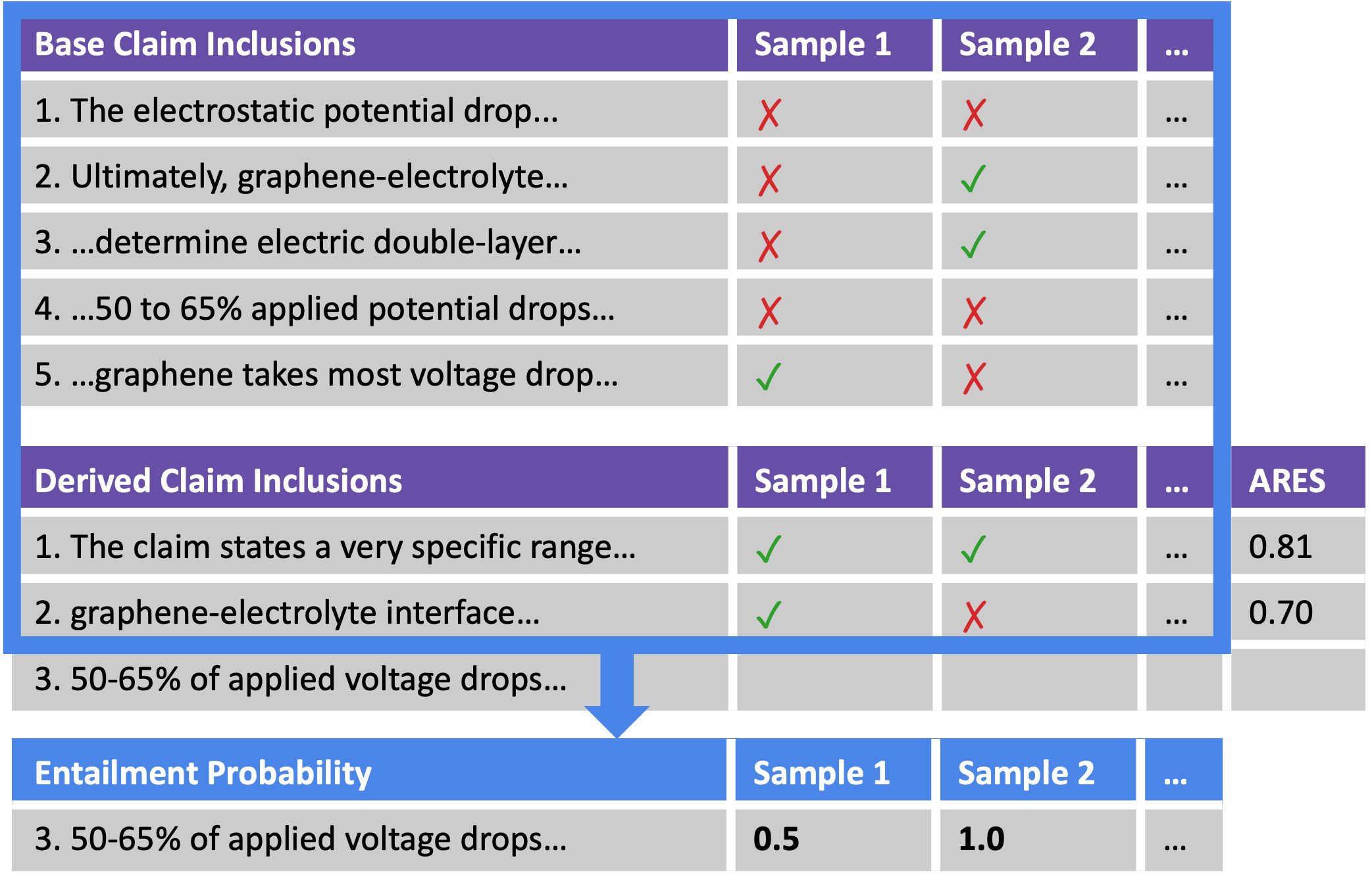
(b) The ARES score for that claim is then the average of all those entailment rates for all the samples.
(c) In parallel, we sample from the entailment rate for the claim in each sample to decide whether or not to include it when certifying future claims for that sample.

Now that we have decided if we want to include this new derived claim in each sample, we can then use the inclusion/exclusion of the new claim to compute the estimated soundness rate of the next derived claim.
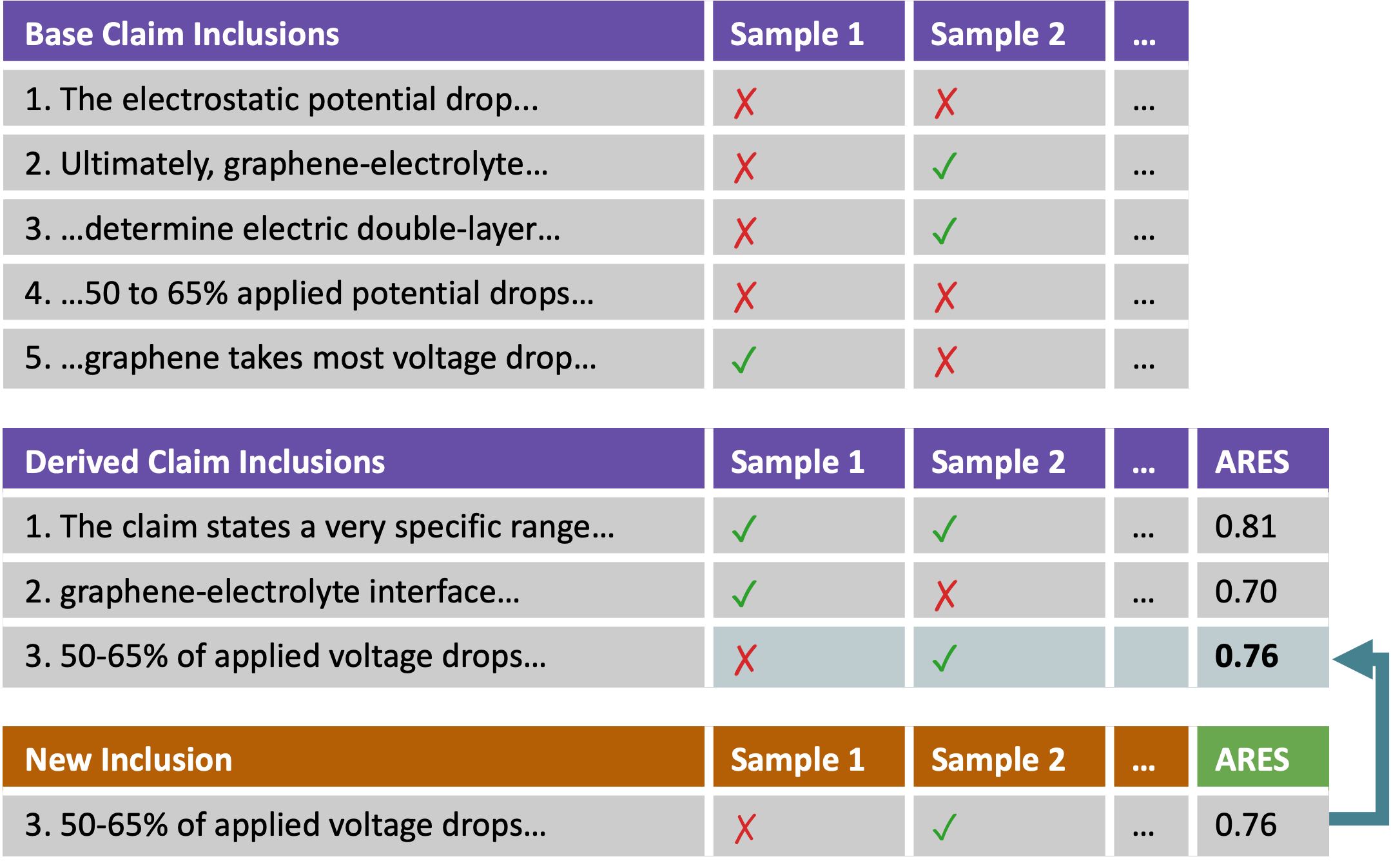
(d) We do this iteratively from the first derived claim to the last, until all claims in the reasoning chain are certified.
ARES Excels in Long Reasoning Chains with Propagated Errors
Existing datasets for LLM reasoning error detection often only label the first error in a chain, typically covering ungrounded statements or invalid derivations. To evaluate whether ARES can detect all error types—including propagated ones—we construct synthetic datasets with long reasoning chains where a single early mistake causes all subsequent steps to become unsound.
Construction is simple: given a ground-truth chain that iteratively applies rules from context, we remove one rule. When the model incorrectly applies this missing rule, every following step becomes an error.
We build two synthetic datasets—ClaimTrees (synthetic rules) and CaptainCookRecipes (adapted from CaptainCook4D recipe graphs)—both containing such propagated-error structures.
Across these datasets, ARES reliably identifies downstream propagated errors, while baseline methods degrade significantly for the reasons discussed above.
Example: ClaimTrees
| Claim | Ground Truth |
ARES (Ours) | Entail-Prev | Entail-Base | ROSCOE-LI-Self | ROSCOE-LI-Source | ReCEval-Intra | ReCEval-Inter | LLM-Judge |
|---|---|---|---|---|---|---|---|---|---|
| Context. Rules: H3 → AZ; SG → C6; C6 → GM; VD → H3; G8 → VD; D8 → U8; U8 → DG; DG → G8. Fact: I have D8. … | |||||||||
| Derived Claim 5: I use rule (VD → H3) to derive H3 | ✓ | 0.79 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 6: I use rule (H3 → AZ) to derive AZ | ✓ | 0.82 ✓ | 1.00 ✓ | 1.00 ✓ | 1.00 ✓ | 1.00 ✓ | 1.00 ✓ | 1.00 ✓ | 1.00 ✓ |
| Derived Claim 7: I use rule (AZ → SG) to derive SG | ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ |
| Derived Claim 8: I use rule (SG → C6) to derive C6 | ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ |
Click for CaptainCookRecipes Example
Example: CaptainCookRecipes
| Claim | Ground Truth |
ARES (Ours) | Entail-Prev | Entail-Base | ReCEval-Inter | ReCEval-Intra | ROSCOE-LI-Source | ROSCOE-LI-Self | LLM-Judge |
|---|---|---|---|---|---|---|---|---|---|
| Context. Only after putting tomatoes on a serving plate, and if we have all the ingredients, we can then pour the egg mixture into the pan. Only after taking a tomato, and if we have all the ingredients, we can then cut the tomato into two pieces. Only after stopping stirring when it’s nearly cooked to let it set into an omelette, and if we have all the ingredients, we can then transfer the omelette to a plate and serve with the tomatoes. Only after chopping 2 tbsp cilantro, and if we have all the ingredients, we can then add the chopped cilantro to the bowl. Only after START, and if we have all the ingredients, we can then add 1/2 tsp ground black pepper to the bowl. We have ground black pepper. We have oil. Only after scooping the tomatoes from the pan, and if we have all the ingredients, we can then put tomatoes on a serving plate. Only after pouring the egg mixture into the pan, and if we have all the ingredients, we can then stir gently so the set egg on the base moves and uncooked egg flows into the space. Only after transferring the omelette to the plate and serving with the tomatoes, and if we have all the ingredients, we can then END. Only after adding the chopped cilantro to the bowl, cracking one egg into a bowl, and adding 1/2 tsp ground black pepper to the bowl, and if we have all the ingredients, we can then beat the contents of the bowl. Only after heating 1 tbsp oil in a non-stick frying pan, and if we have all the ingredients, we can then cook the tomatoes cut-side down until softened and colored. Only after START, and if we have all the ingredients, we can then crack one egg into a bowl. Only after cooking the tomatoes cut-side down until softened and colored, and if we have all the ingredients, we can then scoop the tomatoes from the pan. Only after START, and if we have all the ingredients, we can then take a tomato. Only after beating the bowl contents and cutting the tomato into two pieces, and if we have all the ingredients, we can then heat 1 tbsp oil in a non-stick frying pan. We have egg. Only after START, and if we have all the ingredients, we can then chop 2 tbsp cilantro. Only after stirring gently so the set egg moves and uncooked egg flows, and if we have all the ingredients, we can then stop stirring when it’s nearly cooked to let it set into an omelette. We have tomato. We now START. | |||||||||
| Derived Claim 1: We can now Chop 2 tbsp cilantro. | ✗ | 0.35 ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 1.00 ✓ |
| Derived Claim 2: We can now Crack one egg in a bowl. | ✓ | 0.85 ✓ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 3: We can now Take a tomato. | ✓ | 0.98 ✓ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 4: We can now Add 1/2 tsp ground black pepper to the bowl. | ✓ | 0.80 ✓ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 1.00 ✓ |
| Derived Claim 5: We can now Add the chopped cilantro to the bowl. | ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 6: We can now Cut the tomato into two pieces. | ✓ | 0.96 ✓ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 7: We can now Beat the contents of the bowl. | ✗ | 0.01 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 8: We can now Heat 1 tbsp oil in a non-stick pan. | ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 9: We can now Cook tomatoes cut-side down until softened and colored. | ✗ | 0.01 ✗ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 10: We can now Scoop the tomatoes from the pan. | ✗ | 0.21 ✗ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 11: We can now Put tomatoes on a serving plate. | ✗ | 0.18 ✗ | 1.00 ✓ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 12: We can now Pour the egg mixture into the pan. | ✗ | 0.18 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 1.00 ✓ |
| Derived Claim 13: We can now Stir gently so set egg moves and uncooked egg flows. | ✗ | 0.19 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 1.00 ✓ |
| Derived Claim 14: We can now Stop stirring to let it set into an omelette. | ✗ | 0.19 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 15: We can now Transfer the omelette to the plate and serve with tomatoes. | ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
| Derived Claim 16: We can now END. | ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ | 0.00 ✗ | 0.00 ✗ | 1.00 ✓ |
We can also see that ARES can robustly identify error propagations in long reasoning chains in ClaimTrees up to even chains with 50 steps.
ARES detects more errors on diverse benchmarks
We systemmatically compare ARES with all baselines on PRMBench and DeltaBench in addition to our synthetic datasets ClaimTrees and CaptainCookRecipes. We report Macro-F1 on error detection by thresholding the soundness scores from each method based on a 5-fold cross validation.
ARES detects the most errors across all datasets when using GPT-4o-mini as the entailment model, with especially strong gains on synthetic datasets where propagated errors are known. On CaptainCookRecipes, which contains fewer propagated errors than the linear chains in ClaimTrees, Entail-Prev performs only slightly worse, and the fuzzier cooking logic makes perfect reasoning harder for ARES. On DeltaBench, LLM-Judge matches ARES and ROSCOE-Inter follows, likely because the first error is reliably labeled while propagated errors are not consistently treated as unsound. For PRMBench, the shorter chains (≈10 claims) and fewer multi-premise errors make the task easier, narrowing the gap between methods.
Conclusion
In this blog post, we showed that ARES offers a novel approach to inductively assess reasoning soundness by probabilistically considering only previous sound claims as premises. It is sample efficient and provides a more principled and reliable method for detecting errors in reasoning chains.
For more details, see our paper and code.
Citation
@inproceedings{
you2025probabilistic,
title={Probabilistic Soundness Guarantees in {LLM} Reasoning Chains},
author={Weiqiu You and Anton Xue and Shreya Havaldar and Delip Rao and Helen Jin and Chris Callison-Burch and Eric Wong},
booktitle={The 2025 Conference on Empirical Methods in Natural Language Processing},
year={2025},
url={https://arxiv.org/abs/2507.12948}
}